|
Dave Harris R was mentioned first in Bergsonism. Weyl's reading of R was also a major influence though -- we need to extend Plotnitsky on this. We can explore more implications of R space -- rhizomatic multiplicities, smooth space, links with 'fibre bundle topology and gauge field theory'. The ref to R in Bergsonism relates to the differences between quantitative and qualitative multiplicities, as a solution to the old issue of the One and the multiple. For D, the discrete multiplicity has its own metric, while the continuous has an external metrical principle -- phenomena unfolding within, or external forces. D refers to both R and Weyl's book (Space, Time, Matter) -- the first detailed exposition of Einstein's general theory and the first attempt at unified field theory. D says Husserl was also influenced by R. But W was then ignored. Calamari says he is crucial -- eg in moving from Leibniz monads to nomads,and to developing the notion of a plane of immanence which resembles modern physico-mathematical space. D recognizes that R is both a mathematician and a physicist , especially after Einstein. D talks about the Riemann abstract machine, and says that the notion of multiplicity is both physical and mathematical in Riemann. This is a recognition of mathematics and physics belong together, borne out by Riemann's own work which included attempts to elaborate a unified theory of physical forces. The famed habilitation lecture established topology but also discussed the physical applications of the idea of a manifold, the basis of an infinite number of geometries, which have the specifically non euclidean ones as a subset. But this implies a geometry of physical space, and was a contribution to an earlier tradition, which included W. D went on to argue that the debate between Einstein and Bergson really depended upon different notions of the Riemann theory of manifolds. D says that Riemann saw things, any kind of objects whether empirical or a state of things, as multiplicities defined by various parameters which determine them, which makes the manifold exceed specific domains of application. W also stresses the many uses of the concept of manifold in the natural sciences: it can be used to define geometric entities, phenomena, states of things, sensible objects, physical systems. The various coordinates or variables, dimensions, define these objects, so an ideal gas is two dimensional because it is determined by two variables, pressure and temperature, while colours have three dimensions, adding quality and intensity [to frequency?]. D is endorsing this widespread implication when he says '"everything is a multiplicity insofar as it incarnates an Idea"' (64) [which seems to be rather different and suggests some alternate determination as well as the dimensions?]. Here, the substantive notion of multiplicity is connected to ' the transcendental field of virtual Ideas' (65), making it even more autonomous and irreducible, but it retains a connection to empirical determination 'or actualization', as a matter of 'the differentiation and genesis' of '"real [spatial temporal] relations and actual terms"' [citing Difference and Repetition, 236]. This also implies a 'fundamental immanence'. In this way the Idea becomes 'a concrete universal'. W said the same of Riemann only in the field of maths and physics. So the Idea becomes 'a substantive (virtual) multiplicity', and real actual objects are produced immanently determined by the elements of the multiplicity and their differential [literally] relations or variations [rendered here as dx and dy , dy/dx, and values of dy/dx respectively]. A distribution of singular [only? Not regular?] points corresponds to these relations. All this is consonant with W. Both imply the extension of differential calculus which produces actual objects, phenomena, phase transitions and states of things [apparently, singular points play particular roles in phase transitions]. All this helps us grasp the discussion of the Idea in g. We are told it is an '"n dimensional continuous defined multiplicity"'as when the Idea of colour is a three dimensional multiplicity as above. Dimensions are to be understood as variables or coordinates, continuity as the relations between changes in the variables, which may take different mathematical forms. There is a reciprocal determination so that elements cannot change unless the multiplicity changes. The example of the colour shows the debt to W. The particular insistence on the possibility of a quadratic form of differentials makes explicit the definition of the Riemann Ian manifold. This is what is also found in Bergson ism, where things are actual multiplicities dependent on the virtual multiplicities and the differential relations and points that they embody. There is no other actual state of things. These commentaries seems to be based on an excerpt from W, one where he is closely quoting Riemann's habilitation lecture, which emphasizes this last connection with the physical world, rendered as the connection between geometry and physics and the nature of physical space. W thinks the distinction between discrete and continuous manifolds is important. Discrete manifolds have single isolated elements, determined by the number of elements belonging to it, with a metrical principle inherent in it, something arising from the concept of the number [apparently, this was part of the problem of discussing infinitely small space]. The continuous manifold has a ground or principle outside it in the form of binding forces: [if space is a discrete multiplicity it is self sufficient, and if a continuous one it must have some external dimension which shapes it]. Apparently, quantum mechanics tends to assume that space is discrete, but both Riemann and Einstein imply otherwise. [as in Plotnitsky on residential flats]. D seems to borrow from W in Bergsonism, although he inserts a quotation from Riemann, drawing from the concluding part which they had in common. This concluding part concerned applications to space and which geometry is consistent with the empirical world. This provides the distinction between discrete and continuous, or quantitative magnitudes and spatial topological magnitudes with particular importance. Riemann is actually arguing that the geometry of physical space cannot be determined a priori, and that what is normally taken as real space is probably a special case of manifold, one which is three dimensional, but purely topological, that is devoid of any form, before the introduction of anything that would provide metric determination. This means we must examine the physical forces at work in space to solve the problem of the geometry of space instead of presuming any geometry as an axiom—as euclidean or somehow indifferent to matter which it merely contains. D preserves this twofold character in his own work—the multiplicity can be a purely 'informal (topological)' (69) and autonomous Idea, and also something that is necessarily connected to actual space and physical forces. We see this twofold nature in the notions of a rhizomatic multiplicity and a smooth space in ATP. So smooth space becomes amorphous and non formal, while rhizomes have a metrical principle acting on them from outside, or in the physical phenomena which inhabit them. We find these laws of nature in the infinitely small, apparently, and this reveals a further relationship between Riemann and Leibniz. The implication is that the physical laws can be expressed through differential equations and the differential calculus. Differential geometry emerges by extending the calculus [well done me - I suspected this]. Differential equations will therefore describe natural laws. The second implication is that natural forces act by continuous action, 'that is, by local (infinitesimal) contact' [now I get it] which gets transmitted through the surrounding space. We need differential equations because changes depend on several variables not just one as in classical newtonian mechanics, which also had an idea of action at a distance, the instantaneous transmission of force: Riemann sees mathematical physics as a matter of fields, which he anticipated before Faraday and Maxwell. Deleuze discusses this, mentioning W, in his book on Leibniz, where he agrees that differential equations explain the laws of nature [I have always been puzzled by this interest in the differential equation—now it makes sense]. He also says that the differential links physical reality and mathematical calculus. He has grasped the necessity from this from Riemann and W. Riemann's support for Leibniz can also be understood as an opposition to Newton and the mechanical model, and more as a support for field theories. Again, this would imply that the infinitesimal explains the behaviour of the external world, 'infinitely near action', implying the 'local intrinsic construction of space' (71) as contact interactions propagate along the lines of force or field lines. Bodies no longer act bi-univocally but are affected by the continuous space or field between them. It is this that leads to the 'continuous-discontinuous dichotomy', and also challenges scientific reductionism [mechanism anyway?]. There, however, Riemann and Leibniz also diverge, Deleuze argues, over the issue of the monad. [NB the monad can be an isolated particle] Here, the 'mathematician and philosopher Gilles Châtelet' is cited. C addressed the implications of Riemann in the last section of the habilitation lecture, discussing the implications for the monad of the continuous-discontinuous dichotomy. [It seems that if space is a continuous manifold, there must be communication between monads, because signals would be transmitted from proximate states] (72). There must be local interactions or communications in continuous manifolds, apparently as in Maxwell and Einstein—it is an extension of the idea of action by contact. There can therefore be no closure around monads [apparently Leibniz agreed with the idea of action by contact but saw it as something representing only extrinsic movement, but, monads include the totality of the world, so there can be no genuinely external action, only interaction between monads]. Thus Riemann leads to the challenge to closure and a new openness of communication and coexistence. For Deleuze, C is useful in arguing that differentiation propagates step by step in a community of monads, through tactile relations or connections. C understands connection in the modern mathematical and physical sense, involving a theory of fibre bundles for maths, or gauge field theories for physics. Again, W extending Riemann and linking with Einstein's general theory suggested this [although so did other mathematicians, cited on page 74] [much seems to turn on debates about incorporating work on parallel transport of vectors into Riemann notion of space as a manifold with its own autonomous properties.] W did this by thinking of parallelism as a matter of connection between manifolds as a 'projective' or 'conformal' nature [aka 'affine connection' -- wikipedia defines this as 'an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space', and there is a diagram: 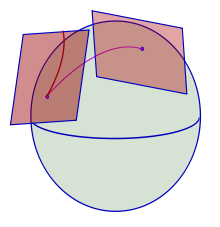 An affine connection on the sphere rolls the affine tangent plane from one point to another. As it does so, the point of contact traces out a curve in the plane: the development.. The term was originally used to describe the displacement of vectors in 'affine' [tangent] spaces, but W. saw that there might be a physical process involved in field theory, perhaps explaining interactions between gravity and electromagnetism. First Riemann had to be read as a thorough rejection of geometry at a distance, 'the possibility of a direct comparison of lengths (specifically, the length of vectors) located at distant points'(74-5). W argued instead that spatial and temporal lengths were path dependent, with local changes in the scale: length therefore became relative, and 'variable scale factors' (75) became important. This would lead to 'local gauge theory'[gauge seems to be something invariant, irrespective of any particular choice of unit length or gauge {sic}]. Einstein apparently argued that physical observations contradicted this idea, leading to further research by W. 'two new fundamental interactions' had been identified by then, the weak and the strong, which opened possibilities for application to quantum mechanics, and apparently this is the basis of modern gauge theory. That led to possible unifications between the interactions in quantum field theory and it now constitutes the standard model in particle physics. Back at the mathematical level, the idea of connections produce the theory of 'topological fibred spaces', again with global implications for understanding connections. We can think of a fibre bundle as an enlarged topological space. There is a base space, an n-dimensional manifold and a total space above it which has a group structure [pass]. Fibers correspond to points on the base space [and they also connect the two levels of space to produce a total space]. In the simplest example, a product space explains a total space as a product of the base space and the fibres -- as in a cylinder, with a circle as base space and a line segment as a fibre. As an additional complication, each fibre itself has m dimensions, so a fibre bundle is not a simple multi dimensional space but an M plus N dimensional space. The way the fibers work is through 'bundle projection (a continuous map)' (76), a relation that can be described as extrinsic but not external. More grippingly, the total space does not just have the basis space embedded in it and is not reducible to base space. Each fibre adds extra dimensions, so a bundle connection is a geometric structure in its own right, and [as continuous space?] helps us deal with the relations between infinitesimally neighbouring fibers. The connections with Riemann and Einstein were not realized at first, but eventually, gauge theory could be related to fibre bundle topology as a further deep connection between physics and maths. There is also a link with general relativity theory. In quantum field theory, quantum particles must interact with a field in order to exist at all, so those particles themselves can be grasped as interactions between matter and force. If a quantum particle interacts with a gauge field [some additional force field?] we can see the effects in terms of changes in the internal states of the particle , such as the 'phase change in the wave function'. Originally, it was thought that the intensity of the electromagnetic field caused this change. Mathematics was much more interested in the potential, produced by differences in particular electrical or magnetic vectors which produced a '"tension"': this is a gauge potential. However potentials have always been seen as ambiguous in physics, even arbitrary. It is not sure if they are physically entities or just convenient mathematical devices ['conventional and arbitrary']. It seems that modern thinking sees potentials as having physical realities because they can produce effects that are not entirely attributable to the field strength. It is now thought that the phase differences of quantum particles are physically determined by the gauge potentials, that field strength is a quantity derived from these potentials, and that the potentials cause the changes. Later heroes demonstrated that gauge fields can be better understood as 'principle fibre bundles'. The base space is the space-time manifold, and the total space shows the dynamics of interacting matter and force quantum fields [matter fields are now seen as 'associated vector fields.]. Each fibre can then be seen to correspond to the 'internal symmetry space' of quantum fields [this is where it gets its extra dimension from]. We can also understand that total space of the fibre bundle as a space of phases of a quantum particle as it moves through space and time and interacts with a quantum field. These phase differences are determined by gauge potentials, so gauge potentials are identified with bundle connections, or changes of phase along a path. The strength of the gauge field is connected to the curvature of the connection [apparently 'phase changes imply either curvature of the connection to be nonzero']. We can think of this as twists in the fibre bundle, producing more than just a simple or trivial connection. So the paths of the monads in space can be seen like this, related to the fibers constituting the space of phases. These will synthesise the dynamics of fundamental interactions. The potentials arising from connection create the vertical particles of the interaction field, and its curvature extends the notion of captures, from the trivial and from Cartesian grids. Space therefore becomes heterogeneous, according to C, an open space of virtual potentials and intensities of matter, a necessary connection between monadic particles and fibers or quantum fields, all of which are affected by others outside them. Interactions of matter and force will affect each fibre [and particle?]. Apparently everything depends on seeing a (mathematical) connection as involving a (physical) potential. The idea of open space in Riemann is retained, and monadic perspectives overcome. [Fascinating, I wish I could understand this more fully]. Deleuze apparently summarizes all this in a short passage in the Leibniz book, discussing the new monadology in mathematics, which he describes apparently [on page 81] as a matter of monads testing their paths and entering into synthesis with other paths through a process of capture. Thus modern developments in science help overcome the important restriction of absolute closure in Leibniz, and confirms the progress made by' neo leibnizianism'. The open world in constant becoming is the chaosmos, where beings are pushed apart and connections kept open through divergent series and '"incompossible totalities"' [citing page 81 again]. The world is open not to something external and supplementary but to a field of interactions. Thus we can develop a nomadological perspective instead, as Plotnitsky puts it, the ideality of striated space vs. the realism of smooth space. The notion of rhizomatic multiplicity also draws upon contemporary notions of interactions and connections of heterogeneous elements. The idea of Riemannian space as a patchwork indicates this. Deleuze sees interactions as in gauge theory, with space as open, a matter of '" extrinsic coexistence"', or a 'plane or "milieu of exteriority"', extrinsic [but not external]. Nor do they have any 'supplementary dimensions of embedding'(81). Technically this means that open spaces are matters of accumulation, not at all like euclidean conjunction, which implies overlaying each point with a tangent euclidean space [I thought this was what Riemann argued at one stage] —for Deleuze, this would still imply that smooth space was still embedded in homogeneous and striated space. This apparently is an intervention with the earlier debate about Riemann and parallelism summarized above. The best way to understand Deleuzian fields and multiplicities is as a non trivial fibre bundle, with the base space corresponding to the multiplicities, and an additional total space composed of internal but extra dimensions of interactions and connections, a field of '"heterogeneous potentials and intensities"' [quoting Difference and Repetition, p.50]. This field of interaction and connections is not an external space for the multiplicities, but rather a necessary milieu. Deleuze thinks that even Leibniz was forced to talk about a minimal outside for the monads, although he saw it as complementary. Deleuze goes on to describe complementarity here in terms of the 'topological property of "unilaterality"' (82), that is '"a torsion of the world, an infinite fold that can be unwrapped' but in a particular way: the other side of the fold should not be seen as exterior to the monads but '"as the exterior or outside of its own interiortiy"', a construction like that of the Mobius strip, already described as a non trivial fibre bundle [above, but I did not mention that]. Deleuze had already, in the Logic of Sense, argued the 'outside' of sense is like a Mobius strip that we need to understand by splitting it, unfolding in its length, untwisting it. This would then agree that unilateratality would become an extrinsic or relational property [something to do with in extrinsic action, introducing no external forces]: the dimension of sense seen from the outside is folded like this. Since the characteristics of the Mobius strip are also intrinsic, this shows that the extrinsic is strictly complementary [apparently the extrinsic refers to unilaterality, and the intrinsic to non-orientability, which might be another term referring to folding or twisting]. This is not to say that the outside is not different to the monad. The same might be said about the relations between the multiplicities and the field—there is an extrinsic outside dimension of openness, but also 'a strict complementarity that prevents any kind of transcendence'(83). The field of interactions and connections can be seen as the '"plane of consistency" of multiplicities, which defines precisely their internal exteriority; that is, of pure immanence'. The plane of consistency is actually the outside of all multiplicities. Its dimensions increase every time connections are made on it, but it is at the same time 'a single, pure plane of immanence'. It is neither an external outside, nor an internal inside: it is instead a twisted fibre bundle, correlated to the contemporary idea in physical science of a physico-mathematical space. Deleuze page |