| Notes
on: Deleuze, G. (2006) The Fold
Leibniz and the Baroque, Foreword and
translation by Tom Conley. London: Continuum Dave Harris [Another plain person's guide I fear. Obscure and clever stuff. I did a bit of homework for some of it, including reading a chapter on Leibniz's calculus (original here, my notes here), and a very helpful article by Stenner on Whitehead here). Translator's foreword There had been a number of attempts to classify and arrange aesthetic styles, often in a way based on botany. However some analysts saw the styles as profoundly interconnecting, and challenged the idea of periodization. The baroque raises particular difficulties because it displays several interconnecting themes and tropes. It also described natural events as well as artistic ones. Deleuze follows the notion of interpenetration and sees the baroque in arts, science, maths and philosophy among others. The style of this book is relaxed and personal, 'without pretension' (xi). Deleuze chooses Leibniz as the most comprehensive philosopher. The main theme of the baroque is the fold, in all its different varieties, to include pleats, curves and twists. The mathematics introduces new conceptions of point of view. The philosophy rethinks many of the Cartesian distinctions as folds. The mystical experiences associated with the baroque gothic is developed in terms of discussion of the event as 'the virtual sensation of a somatic moment of totalization and dispersion' (xii). These moments appear in novels as 'a seriality of epiphany', in science as the recognition of infinity and the universality of flow, in Whitehead, it is a matter of duration that produces concrete objects. For Deleuze, 'an event unfolds from the union of a perception and the duration of a fan… that unites and disperses a word... and an object... when it swirls the atmosphere' (xiii). Deleuze develops these ideas by identifying himself with Leibniz in a form of indirect discourse, as he has done with other authors like Nietzsche, Spinoza or Bergson. He cites Leibniz often in his own work, especially Logic of Sense. For him, Leibniz develops concepts that link the organic and inorganic, discusses multiplicity and inflection in the production of events, and identifies vibrations with harmonics [and resonances, no doubt]: the latter helps us avoid the usual hierarchies in the development of concepts. A sensuous view of the world results. Leibniz's work produced many themes that have informed modern science and arts, specially through the notion of 'habitat'. Deleuze is influenced by Proust's style of dispersion of the elements of a whole, alluding to multiplicity, according to his commentary, the play of textual machines. This is directly related to Leibniz on the monad as the 'inclusion of the subject in the predicate'(xv). This notion dethrones all conventional boundaries and hierarchies, and leaves the world as 'a chaotic cosmos or chaosmos'. Human beings cease to be the privileged subjects, and they have to acknowledge there are connections with inorganic material. This has led to later work on geophilosophy or absolute deterritorialization. Conley argues that this applies to the domination of liberal capitalism. Geopolitics in What is Philosophy continues this argument as a demonstration of the importance of monadic thinking. Deleuze also pursue some of these implications at the end of this book and talks about, for example 'the radiation of musical waves'(xvi) surrounding monads. The theme of the baroque house is also used throughout. Artists and musicians have been inspired by this sort of argument, and have sought to 'transform monadology into nomadology', especially to connect private space and public world. They also pursue folding, unfolding and refolding to account for perceptions of the world as having shrunk, while organic and biological matters have become more important. Ironically, Leibniz has also provided themes that have helped the development of capitalism. Nevertheless, thinking in terms of folds that traverse regions of the world can help us find our way to 'sensibilities not under the yoke of liberal democracy' (xvii). This might seem optimistic and impractical, and this book should be red as offering only hypothetical approaches to problems, and utopian thought. 'Leibniz is political because he is utopian' (xviii), and can not be localized. [The fold refers to the virtual]. Leibniz develops the mapping of baroque territories, which are infinitely folded and also infinitely porous [I think of Mandelbrot sets]. This is the opposite of Cartesian thinking, with its knowing self and its two dimensional map of reality. For Deleuze, the subject is best seen 'as a play of folds' (xix). There are also new conceptions of the object, moving away from the metaphor of the stamped repetition towards a notion of 'a "continuous variation of matter"'(xx) The style in this book involve simple sentences and transparent expressions [!]. We are to read the edges or pleats of the sentence. The conversational tone is an attempt to dethrone the authority of the writer. Concepts are linked into serial chains. There is a deliberate attempt to conflate subject and predicate. There are different lexical constructions. The idea is to keep the subject and the predicate 'from being an attribute of the other'. The style also 'promotes confusion of form and sign'. The components of the sentences invites readers to reconnect them, 'to produce mobile effects'. The idea is to combine folding and unfolding, working towards principles, at the same time unfolding them, to produce serialities. There is no attempt to reproduce original concepts in stamped repetitions. There is no narrative aimed at reaching some underlying truth. Instead there is 'the modulated flow, as it were, of concept-sentence-units, which flatten illusion that generally accompanies the rhetoric of argument or narrative' (xxi). The chapters can be read in any order. Individual conclusions are 'enveloped everywhere in the "machinic" manner of the text'. Chapter one. The pleats of matter The baroque refers to a principle of the endless production of folds. In this case, other trends and other folds from other countries are also included [more on these different types of fold to come]. Baroque folds extend to infinity and on two levels, matter, and the soul. [Already we can see this sort of itemized style, with separate sentences that have some sort of unspecified relationship to each other—in some cases, alternative formulations, models and metaphors are being developed; in others, Leibniz's terms are being expounded and applied] Matter is folded first to accumulate it, and then to organize it [a bit like geological double articulation in Thousand Plateaus], and this is how organs develop. The soul approaches the glory of god [infinite knowledge?] following its folds to infinity. The multiple can be defined as something which is folded in many ways, as well as having many parts. One kind of folding gives you the labyrinth. Matter and soul are connected as two levels, although there are also levels in each as well. This can be demonstrated with the diagram of the baroque house on page five.  The soul occupies a closed room, while matter is open through several windows, for example the five senses. Information from matter is projected on to the darker background of the room of the soul [later, explicitly, as a camera obscura]. The result is 'an innate form of knowledge' (4), which can be further developed through additional vibrations and oscillations of matter. [It seems conventional to describe the folds in matter as pleats, and those in the soul as folds. Some ontological implications might follow, perhaps explaining the apparent greater solidity of matter, for example?]. We can see the connection between the two levels as another fold [nothing is sharply separated or divided as we shall see]. Leibniz uses the metaphor of the veins in marble [veins in a statue made of marble that is], sometimes to describe pleats of matter that surround living beings, sometimes to refer to innate ideas in the soul, to convey the notion of statues trapped in marble. Various commentators have described the baroque house as having particular architectural features (4), or displaying a particular liking for the curvilinear. Leibniz saw the universe as circular and as shaped by 'the fluidity of matter, the elasticity of bodies, and motivating spirit as a mechanism'(5). Matter moves along tangents, but is also compressed to make it curvilinear or spinning, linking with surrounding areas. The results is 'little vortices in a maelstrom', with more and more vortices inside them [like a Mandelbrot set]. This makes matter 'infinitely porous, spongy, or cavernous', with bodies internally pierced and penetrated by a fluid. This is perfect or absolute fluidity, 'the absence of coherence or cohesion' (6). There is no inherent separability of bodies in matter, and no absolute properties either, but only those produced by surrounding forces in a relative form, such as hardness or elasticity. In mathematical terms, there are no 'separable minima', no separate points in a line. Coherence takes the form of a fold, a complex of folds rather than separate parts. Folding accounts for the division of the continuous, and there are an infinite number of folds. The fold as the smallest unit of matter. Folds can be aggregated to produce mass. There is no absolute unfolding either, only the path from one fold to the next. Folding implies that contrary forces are being combined. The folding may be the result of complex interactions of different forces, say the folds in rock. Overall, we should consider matter as 'the "origami"… the art of folding paper' (7). This approach also shows 'the affinity of matter with life and organisms'. Organic folds can be specific, but we see the connections at the embryo logical level, with folding as a prelude to cell division, and the development of 'invagination' [the formation of enclosures, eg tubes]. This is not a regular process, because the folds are determined by different forces, each of which brings a new cohesion at a particular level. However, the mechanisms that produce matter [specific masses of matter] have to be motivated, and we find '"a spirit in matter"' at all levels. Matter changes over time as the discharge of the spirit. We can explain this in terms of 'tension-release and contraction-dilation'[a definite echo of Bergson here as well?]. We do not need to start with some original void out of which matter condenses. The matter in the lower floor does differ, however, according to whether folding is endogenous or exogenous [the difference between organic and inorganic matter respectively] endogenous folding in living beings takes the form of evolution, for example. Nevertheless, there are no other fundamental differences: 'matter is all one' (8). Sometimes we think of the forces operating on matter as entirely material or mechanical, not involving souls, and these two act in their own domains: they can even 'transform raw matter into organic matter'—these are the plastic forces, to add to the elastic and compressive ones. [There seems to be this two stage articulation involved again, creating first masses, then organisms]. However, we are then told that organs are different in that they're always produced from other organs before them! [This seems to be used to explain organisms as realities in their own right]. The difference is between mechanisms on the one hand and machines on the other. Again there is a suggestion that the one can lead to the other if a mechanism is adequately developed so as to be capable of being assembled into a machine, already 'infinitely' or 'adequately' machined [looks dangerously like a tautology to me]. This process requires a certain kind of transformative folding. With inorganic mechanisms, a series of external determinations are required to cross thresholds, but living organisms are preformed so as to have 'an internal destiny' that produces machines 'all the way to infinity' (8). We can see this as 'a difference of vector' (9), one producing greater masses and statistical mechanism, the other smaller masses and more individuated machines. Leibniz had to rely on the notion of a soul to produce individuation, however, which was distinguished from a more abstract kind of individuation, 'a container of coherence or cohesion'. This is also 'an invagination of the outside', but organic invaginations require the more abstract kind of interiority to be possible. Organic interiors can then be changed by the 'principle of individuation', while other individual enclosures simply show the affects of folding [the example is individual leaves of the tree]. Folding - unfolding involves not just tension-release or contraction-dilation 'but enveloping - developing, involution - evolution'. Organisms can fold and unfold their own parts according to a predetermined degree of development. Birth and death can be seen in terms of folding [of internal 'seeds'] and unfolding, returning back to an involuted state, respectively. Unfolding also increases, but folding diminishes and reduces, although this is not just a simple quantitative matter. In particular, the parts of the machine are all necessary, even though the smaller ones don't just replicate the whole. This can explain metamorphosis: it is clear that the change from caterpillar to butterfly is a form of unfolding, [the butterfly is folded into the caterpillar] but it's not just a standard quantitative difference between them. The animals [the organic] are in this sense doubles, with potential to change by supplying particular parts in particular relations. The notion of doubling or envelopement produces an notion of scale akin to Russian dolls—each unit has another unit inside it. It is also a matter of internal envelopment rather than external impact. This means that inorganic folds are simple and direct, but organic ones are composite, mediated by the interior. However, masses and organisms 'are strictly coextensive' (10). The elastic and the plastic forces both produce folds, but again one does not turn into the other directly, so there is no automatic generation of the plastic, so no notion of universal spirit. Clearly, living beings are not the same as exterior sites or contexts, but live within them. Leibniz sees organic folds as operating in between inorganic ones, as a ubiquitous development [this apparently has something to do with his principles of reason as well]. This notion, especially of doubling or 'pre- formation and duplication' has been challenged by modern biology in favour of evolution as epigenesis, a general design, altering according to the environment, a shift from general to special, differentiation produced by exterior surroundings. However there is some connection in that preformism still operates with the notion of potential, and modern biology still thinks of the organism as a fold, or a folding. [Deleuze says that the first term is simply the only way that the process could be thought out in the 17th century]. They do differ in terms of whether folding just modifies the same animal, or produces some irreducible product. The modern conception sees folding as emerging from a relatively smooth surface rather than from another fold, an original differentiation, not a difference of another differentiation already. Deleuze thinks the 17th century notion might still have some mileage. Going back to the baroque house, masses and organisms to fill the lower level. Organisms at least already have souls, as we have seen, that guide their development, but these are localized souls, developed from point of view 'in the body' (11). The plastic forces form unities of synthesis, but these are mediated through an internal principle for organic forces, and simply an external one for inorganic. This is a kind of animism: life, and souls, are everywhere. Organisms must have some source of their tremendous power to fold and unfold themselves forever. This process takes on a particular 'degree of unity (mind)'(12) as human beings develop. The human soul becomes a reasonable soul, but Leibniz did not know if this is a natural process or a divine intervention. This sort of elevation is represented by the upper storey. Reasonable souls fall back into matter at death, and might be resurrected at the last judgement. These possibilities are represented in baroque architecture including ceiling paintings, where they appear as two vectors separating levels of the same world. This is not the real distinction, however, partly because it also exists in organisms at the lower level. However, it is a different notion from localization in bodies, to a projection outside of bodies focusing on bodies. It is the acquisition of reasonableness that means that souls can change levels. Similar arguments apply to notions of ordinary distinctness of separateness: it always follows the model of localization turning into projection, the difference between mechanical derivative forces operating on masses to unify them mechanically, and primitive forces, whole 'immaterial principles of life' (13) that operate on the inside, as an analogy with the mind. Again souls exist everywhere, even in inorganic matter: inorganic matter projects on to sites somewhere else as well [higher levels of physical force?]. If bodies follow curves [I am not at all sure why they should, although I know that Leibniz was particularly interested in curves, of course], that is a result of compressive or elastic forces affecting surrounding bodies. Without these forces, 'the body would follow the straight tangent'. Even so, the unity of the movement along the curve is still difficult to explain by mechanical forces—therefore it is 'an affair of the soul, and almost of a conscience' (14). So curves are produced by some higher internal unity, originating on the other floor where we find laws of curvilinearity, changes of direction and folding, some primitive force. This is what makes curves not just deviant path from straight lines, but something primary, something also referring to interiors, causes of movements in bodies. This is why we need the second floor: windows on the lower floor permit impact from external events, producing folding as pleating, but even for physical matter, there is some internal animation, spontaneous folds, which provide the reason for the pleats. It is this that explains the relation between organisms and animal souls, human souls, bodies and souls in general. Chapter two The folds in the soul The process of inflection produces curves or folds. This idea has been developed by artists such as Klee (below), and this differs from those who operate with more Cartesian spaces, such as Kandinsky.  The point of inflection is where the tangent touches the curve—'the point-fold' (15). For Leibniz, straight lines and curves are always intermingled [at that point, curves become straight line tangents, and presumably, any straight line can be considered as a potential tangent with a curve touching it]. Apparently the notion of a point-fold also has a more general application suggesting that the finite curves are also mixed with each other, so that it is impossible to be precise [Cartesian] about the surface of the body. Concave curves are going to be particularly important, as we shall see, because point of inflection change sides [thus so do points of view?] . We can see the point of inflection 'as an intrinsic singularity'. It is ambiguous, not locatable on [Cartesian] coordinates, and 'weightless', a point between curves [or straight lines and curves]. The inflection that ensues 'is the pure Event of the line or of the point, the Virtual, ideality par excellence' (15-16), something that will happen, but it is not yet in the world, the point of infection is the beginning of the world [classic grandiose terminology] . There are three transformations of inflection [presumably given by mathematics, probably by this guy Cache who gets mentioned a lot].
 Leibniz began to develop such 'baroque mathematics', trying to explain variation itself, beyond particular values, and approaching the infinite [some examples are given using irrational numbers, 18]. Variation can only be depicted as a curve, or, in materialist terms 'the presence of a curved element acts as a cause'. The curve is always there, even if it is intermingled with straight lines [I think the argument is that any point on a line, even a straight one, or the apex of a triangle, can be a point of inflection]. The discovery of pure variation is illustrated by the example of differentiation to infinity [see my plain person's notes on Bos on Leibniz's calculus]. We can also think of the fold as power [not just in the mathematical sense?]. Folds indicate variation. Generalizing, 'Force itself is an act, an act of the fold'(19). [We have a lot of metaphors helping us slide from maths to metaphysics -- no doubt the 2 are connected through the principles of reason again?]. Mathematics increasingly comes to emphasize the notion of a function [roughly, an abstract operator, part of a general move away from concrete values to mathematical expressions, see my notes]. Thus Leibniz is interested not just in unique tangents, but infinite numbers of tangents and infinite curves, a family of tangents, taking a curvilinear shape. This helps us further develop the notion of variability itself, a function which can be seen as 'declining a family of curves, framed by parameters, or inseparable from a series of possible declensions' (20). This is an example of an objectile. We can explain it via the development of industrialism from producing unique objects, moving on to standard objects produced by constancy, turned out as stamps from a mould and the current notion of a 'fluctuation of the norm', incorporating temporal modulation, continuous variation, as opposed to spatial moulds. Leibniz is on to this notion of modulation when describing curves, but he has a more general notion as well, with a qualitative flexibility and modulation. This is apparently a mannerist conception, and it replaces the notion of essence with that of event [it seems pretty similar to the notion of machinic variation producing specific singularities?]. Objects now become objectiles, and the subject changes as well. We can understand this by first of all considering curvatures that produce concavity. With concave curves, it is possible to draw lines to right angles to the tangents of the curve [pointing inwards, so to speak], and where they meet we have a position, site or focus. We can consider this is a point of view, because it represents variation [to think in human terms, an eye placed at that focus could perceive variation]. It is this mathematical notion that underpins an objective form of perspectivism: this is not grounded in the point of view of the subject, but in these more objective points of view. In the terms of Whitehead, (see Stenner's article) we can see individual localized perspectives as producing a sub-ject, but the composition of these localized perspectives produces a new emergent creative body, the superject. The composition and agglomeration, as it were, arises not just from combining points of view in the subjective, [as in spiritual automata], but because 'every point of view is a point of view on variation' (21), if we bear in mind this mathematical notion. Points of view are not integral to human subjects, but predate them. If anything, subjects [in its normal usage] occupy points of view, and they can then apprehend variation or an amorphosis [a deliberately distorted view which make sense only from a particular viewing stance—the skull in my favourite example by Holbein below]. So perspectivism is relativism, but this is not provided by truth appearing to the subject differently. The objective notion instead 'is the very idea of Baroque perspective'.  However, there might be a problem with a concave curve, where a viewpoint is limited, and unable to see infinite variation [like that which continues on either side of the concavity]. This has something to do with Leibniz on indiscernibles: [Wikipedia, god bless it, tells us that this refers to 'an ontological principle that states that there cannot be separate objects or entities that have all their properties in common. It splits into 'The indiscernibility of identicals: For any x and y, if x is identical to y, then x and y have all the same properties' and 'The identity of indiscernibles For any x and y, if x and y have all the same properties, then x is identical to y'. The first one is simply true logically, but the second is controversial. Against the second, 'Max Black has argued against the identity of indiscernibles by counterexample. Notice that to show that the identity of indiscernibles is false, it is sufficient that one provides a model in which there are two distinct (numerically nonidentical) things that have all the same properties. He claimed that in a symmetric universe wherein only two symmetrical spheres exist, the two spheres are two distinct objects even though they have all their properties in common'] [I hope this will become clearer when we go on to talk about the principle of sufficient reason. I think the dilemma is that the principle of indiscernibles does not fit well with the notion of continuity because continuity implies a change in some of the properties, even though the point remains a point?]. Deleuze says that we should not confuse continuity with contiguity. The main implication is that we can explain singularities or unique points in a way that does not contradict the notion of continuousness, as with points of inflection on the curve. To reconcile it with continuousness, though, we have to admit that there are an infinite number of inflections, and therefore an infinite number of points of view. There may always be distances between points of view, as an 'attribute of space', just as there are between points on a continuous curve, but this is not discontinuity, because, 'no void is given between two points of view' (21-22). Continuousness can be seen as continuous repetition of a point or points of view, across space and spatial distances. Varying points of view helps us understand the figures or configuration, most famously when considering conic sections—circle, ellipse, parabola and hyperbola are understood as variations and points of view, ways of mapping flat projections. There is no master point of view, as when we draw a cone using conventional notions of perspective, but varying projections. The cone becomes an objectile, offering curves in a particular relationship [declension] . We can also consider these projections as an unfolding. This unfolding does not contradict folding any more than an invariant contradicts variation: the former is enveloped in the latter, 'just as variation is enveloped in point of view'(22). Because of this relationship between variation and the invariant, there is a law of '"involution"'[that says invariants will be produced in particular circumstances? The example given on page 22 of a rotating triangle is obscure—and what I can see, rotation of points on a figure projects fixed points on to the axis of rotation]. The example of the projections of the cone has been generalized to make the point of view replace the usual centre or focus of perception in conventional perspective, and there are implications for conventional geometry as well. In this new conception, associated with somebody called Serres, objects exist only through their metamorphoses 'or in the declension of their profiles', so perspectivism itself becomes one moment, one truth of relativity '(and not a relativity of what is true)' (23). The point of view becomes a 'power of arranging cases', or the way to manifest reality. It becomes necessary to assign points of view to particular cases, and these can be arranged in a Leibnizian table. This table constructs the options in 'jurisprudence or the art of judgment'. We try to find the best point of view to determine the indeterminate, in the middle of chaos or disorder, as with anamorphosis. This helps us understand inclusion as a mathematical concept, although generalizing from these mathematical concepts require 'a more natural intuition' [what can you make of this as a philosophical argument?] . Similarly, visibility is not entirely similar to point of view. The intuition suggests that something is folded or enveloped not only to provide coherence or cohesion, or mathematical certainties. Instead, we need to talk about 'inclusion or inherence' as 'the final cause of the fold' (24). [This seems to be a connection here with the actualization of the virtual as well? 'What is folded is only virtual and currently exists only in an envelope, in something that envelops it']. Point of view includes, as an agent but not a cause. The condition of closure or envelopment is represented by the lack of windows in the upper floor of the baroque house. It refers to a soul or a subject, something that includes what is apprehended from a point of view, [an generalized kind of] inflection. It follows that it is the soul that folds [at the lower level] and is itself folded. This makes a bit more sense [!] if we see the soul as containing innate ideas, 'pure virtualities, pure powers', arranged as folds in the soul, and put into action. We can then see the whole world as a virtuality existing 'only in the folds of the soul which convey it', realized in the folds of the soul as 'inner pleats' which represent the world. This process of moving 'from inflection to inclusion in a subject', is paralleled with a movement 'from the virtual to the real'. Inflection defines the fold, but inclusion defines the soul which envelops the fold, causes it and completes it. [This basic argument is spelled out and repeated in what follows] We have three kinds of points in these processes, three kinds of singularity. First, the physical point, the point of inflection, or points on the line of inflection. This is an 'elastic or plastic point fold'. This conveys on a mathematical point a new status. The point is still conventionally a part of extension, but is now also a site or a focus, 'a point of conjunction of vectors of curvature' (25). Secondly [?] these points of conjunction are still extended in lines, they are points of position. Thirdly, points can be seen as projections, becoming metaphysical points of 'the soul or the subject', its projected point of view at a higher level. The soul or subject as a metaphysical point is Leibniz's monad, a Neoplatonist term meaning 'the unity that envelops a multiplicity, this multiplicity developing the One in the manner of a "series"'(25). The One envelops and develops, the multiple becomes the folds that are produced by envelopment, and the unfolding by development. All are part of a 'universal Unity that "complicates" them all'[that is produces complexity?]. In this way, the monad can 'give way to a large zone of immanence'. We can understand the fold as a combination of explication, implication, and complication [also discussed in Deleuze on Spinoza, I recall]. Leibniz was able to 'stabilize the concept', by thinking of it in mathematical terms—so that, for example inflection helps us see a series of multiples 'as a convergent infinite series'[each produced by points on the curve, if I understand this correctly, which is by no means guaranteed!] His metaphysics also helped see inclusion as a matter of 'enveloping unity', but at the level of 'an irreducible individual unity'[tied to and based on an individuated point of view?]. The shift towards seeing the importance of infinity is crucial, because it moves away from individual relativism [always possible if individuals are seen as members of the finite series]: the infinite series is a logical notion, and, at the same time, 'the concept that can now only be individual'[I am not sure what this means, unless it means that we can't generalise about infinity? Perhaps it means that human logic has constructed it and that this cannot be relativized?]. In Leibniz's hands, infinity also permits an infinity of individuated souls and points of view. The mathematical basis for the conceptions mean we can abolish pantheism or older notions of immanence [and, somehow, older notions of universal complication—which would all require some unifying god or spirit?]. There are still obscurities [!] There still seem to be master of points of view, for example, in the case of the cone the view of its summit, which help us to grasp the whole group of forms or curves [the only pov which includes all the cone?] . Leibniz seems to suggest this in terms of saying that all the points of view are still connected [which seems to imply that there is no such thing as a fully independent point of view, including a master point of view, since all points of view are connected—'and the entire world is enclosed in the soul from one point of view' (26)]. This is indeed the notion of the world is an infinite curve touching a series of specific curves produced by unique variables. But why does this not yield a universal point of view, and let back in god or universal spirit? How does the all-encompassing world still produce irreducible souls? We turn to a musical metaphor. The 12 notes on the scale can be varied in infinite ways, or, rather produce 'an infinity of [individuated] variations that make it up' (26). In this way, particular sequences must always be understood as being 'in accord with all possible orders' [but what does that weasel 'in accord' actually mean here? Presuppose? Yield to mathematical calculation?]. Each monad is an individual unit, but it also includes a whole series and therefore conveys the entire world [diagram on page 28 reproduced below].  [NB I assume the little curves are supposed to touch at the points of inflection on the big circular curve?] As it expresses its own small region of the world, it expresses the entire world [Spinoza again, surely?] . Two souls do not always have the same region to express. What this means for individuation is not that individuals include the series in a particular way, shaped by a particular region, but the inverse. This is only so far 'a nominal definition of the individual' (27), but it makes the same points that each included soul and points of view can grasp the whole 'infinitely infinite seriality'[a circular argument, because this is what 'included' means in the first place? It is all circular if you ask me, all definitional, all really just a matter of spelling out implication of definitions]. Each individuated grasp it is different and from the different standpoints, but this still helps develop 'a point of view on inflection in general'[we can generalize or philosophize from our own particular points of view, more or less as Leibniz must have done, via mathematics?] We still have problems in deciding exactly what is going on as inflections of the world become inclusion in its subjects, especially if we have continula ambiguities about whether subjects are only parts of the world or 'the world only exists in subjects that include it'. This is where we get to Leibniz's homely analogy about Adam. In the world of Adam the sinner, Adam commits sin. However, this is not the only possible world, only one of the range that god has created: subjects and their worlds are interdependent. Adam's world is a part of Adam as subject, but he is a subject for that world. [I think this means that notions of the universe as a series of curves and all that is found in the soul, but not exclusively]. After all, souls have to be a part of the world created by god [but why does god need them?] and chosen to be realized through Adam. Monads construct their worlds, but not the reason of the series of worlds—another meaning represented by the soul having no windows. [Apparently, Heidegger has borrowed this idea from Leibniz to bleat on about being-in-the-world 28 ]. Some closure is essential so subjects can be for the world, something which '"finitely represents infinity"' (28) [I can only understand this as some psychological necessity to manage infinity, but it might also be that infinity has to be managed in order for actualization to occur]. This makes the world capable of beginning 'over and again in each monad' [but why does the world need monads, without getting hegelian about it all?]. This is how the world and the soul are folded together. Actuality here is defined as the way the soul expresses the world; virtuality becomes what the soul expresses. This is how inflection becomes inclusion, so that 'the virtual can be incarnated or effectuated'. However, some other process of 'realization in matter [is] also required' (29) [I think in order to make sure that matter is autonomous, not just some sort of simple duplication of the folds in the soul]. Chapter three What is Baroque? [Heavy going, with lots of references to artists. I found some illustrations that might help. Sorry if this makes the file slow to load. The argument is that we have to understand baroque architecture if we are to understand Leibniz and the monad—which, increasingly, seems to refer to the upper floor only of the baroque house. God knows how this will help people who do not understand baroque architecture!]. We understand the upper floor of the monad by thinking in terms of projection—the projection of the film in a dark room, or mathematical functions projected from actual calculations in Leibniz's calculus. We can see the same idea in Rauschenberg (example below) where the painting ceases to be a window referring to an external reality, but rather 'an opaque grid of information on which the ciphered line is written' (30).  We can understand the monad as the room on which the camera obscura projects its images, the dark inside, 'completely covered with lines of variable inflection… Moving, living folds'.We can see this dark interior in certain baroque buildings, where light is passed through a series of apertures and mirrors, and the walls and ceilings are covered with painted trompe l'oeuil, as in the Studiolo of Florence (below). In the monad, the inside is disconnected from the outside, from its facade. The facade has doors or windows, even if they are not proper ones, and exhibit 'rarefied matter'. In living monads organic matter does possess a certain relative and unfinished interior dimension, and this the fold through living material makes the concepts of the monad into a metaphysical principle, 'the physical law of phenomena' (31). Outside matter ramifies to infinity, an 'infinite repetition of open linkages', and this can only generate a metaphysics if repetition is closed. Nevertheless, this is not a complete closure, because, as in baroque architecture, interiors have only a relative autonomy, and display a relatively calm and peaceful viewpoint, compared to the 'exacerbated language of the facade' (32). Baroque is what has developed this new harmonious link between inside and facade. The link has been described as the tendency of vector turning on gravity, strongest at the bottom, featuring weighty mass, combined with an elevated weightlessness. We can see the idea in Tintoretto's contrast between angels and mortals ( example below)—The Last Judgement) [although Deleuze has also criticized this painting as not going far enough]. The two levels are linked by analogy. They also described 'a function of an ideal line which is actualized on one level and realized on another' (33).  However, matters are more complex than this [!]. We can see this by considering particular types of the fold. There is the zweifalt [I have translated this as duplex fold and found an illustration from geology below]  This fold both differentiates and is differentiated, indeed, it is the differentiator of difference, [Hedidegger says] rather than of 'a pregiven undifferentiated'. Ideally, it would endlessly fold and unfold on either side, or possibly even unfolding the one only by refolding the other side. Yet there are different sides. [Another example is a poem by Mallarme, and I have had to skip this—apparently, it introduces the notion of the fold of the world as a fan, producing wind which agitates particles of matter, producing degrees of visibility. Another analogy is the notion of a book, with multiple leaves modeling the monad, as a sort of example of 'the unity that creates being, a multiplicity that makes for inclusion'—while the page, possibly, is 'the Event']. Leibniz himself preferred to think of veins marble, teeming with life of the microscopic level, and serving as point of inflection to include that life in the rock, in its layers, another type of folding. This produces, as with the book, the possibility of reading reality, and this is what the monad does: apparently, Leibniz dreamed of acquiring a total book [explaining everything in terms of concepts of the monad and the fold]. This ability to read the visible again connects the inner with the outer, and produces the '"emblems" or allegories dear to the Baroque sensibility' (35): everything is referred onwards to another fold. There is also 'a new regime of light and colour'. We can use Leibniz's notion of the binary, and assign values of one and zero to light and shadow respectively. However, it is not just a simple distinction. Baroque painting, as an image of the monad, does indeed start with darker backgrounds things that 'jump out', colours arising from a common base. This is not a rejection of or opposition to light, however. It is like an internal light, shading towards the dark, offering degrees of clarity and obscurity, including some 'effacement of contour' instead of Cartesian separation and clarity. It is continuum, with god's light at one end, and an infinity of black holes and caverns at the other [then a very obscure bit suggesting that the fold between darkness and light has limits at either end of the continuum?, 36]. Leibniz displays 'the entire German soul', described by Nietzsche as 'full of folds and pleats', not just 'deep'. We can see Leibniz almost as a schizophrenic as his personality manages the tension between the open facade and the hermetic interior [which turns into assessment of him as courteous and open, but also mysterious. The courtesy might be responsible for his tendency to insist that he is working towards '"the best of all sides"', constantly trying to absorb newly discovered twists and turns—37]. Baroque thinkers have always worried about consistency and arbitrariness, and this has led to its being seen as restricted to architecture, or to a particular time, or even a denial that it ever existed—hence this attempt to define its organizing concept, and to locate a place in it to Leibniz. [Various definitions of the baroque are discussed 37-8]. The organizing concept is the fold for Deleuze, and everything that it implies. In this sense, the baroque links to other experiments with folds, including contemporary artists like Hantaï (below),  and can be seen anticipated in earlier work as well like Uccello and the strange habit of covering heads with weird hood-like things -- 'mazzochi' (below).  The problem here is that just about every period and style has used a fold in painting and sculpture. We find it in the orient and the Romanesque. However, only in the Baroque does the fold have 'unlimited freedom whose conditions can be determined' (38), folds with no apparent determinations as in El Greco's Baptism of Christ (below)—'a counterfold of the calf and knee, the knee as an inversion of the calf, confers on the leg an infinite undulation, while the seam of the cloud in the middle transforms it into a double fan…' (38-9).  We can summarize the characteristics of the Baroque 'and the contribution of Leibnizianism to philosophy' (39): The fold, the infinite work or process, the way the fold affects all materials and therefore becomes 'expressive matter', depicting different scales, speeds and vectors, found everywhere in the organic and inorganic, and in this way 'it determines and materializes Form'. Lines inflect. Inside and the outside, separated by an infinite fold between matter and soul, facade and interior. The line becomes something virtual, always dividing itself, and is 'actualized in the soul but realized in matter'. There is a constant production of exteriors and interiors, extension and enclosure. 'An infinite "spontaneity": the outer facade of reception and inner rooms of action'. Baroque architecture offers a new harmony between the principles of bearing and covering. Yet we have to remember that 'what is expressed does not exist outside its expressions'. The high and the low, where the tension between matter and soul [and all the other things] is represented as a division of two levels, both of the same world, separated by the infinite fold. This fold expands greatly on either side, producing further folds, tucks in the inside, protrusions on the outside, pleats of matter, folds in the soul. Baroque art celebrates the textures of matter, including that in a modern form as in Klee, but also includes 'immaterial folds'(40) as 'styles or manners'[reworked as the difference between raw material and force to produce a new 'material - force' to replace the old distinctions between matter and form]. The unfold, which does not just oppose folding, but continues it, as when Hantai folds the canvas irregularly, paints the different surfaces, then unfolds it 'to cause the inner white to circulate'. However, Hantai also experiments with the 'oriental line' [regular folding as in a fan?], producing an alternation between 'the full and the void': the full baroque line would not have voids. Leibniz had a similar problem when developing binary mathematics, considering what the zero might represent—only apparent voids for him. Textures: active or derivative forces act on matter, but passive forces relate to 'the resistance of material or texture'(41), and at the limit, textures cannot be folded. However, normally texture is produced by the way a material is folded, a style [which has got something to do with mannerism, apparently] [Mannerism appears to be an artistic style that usually is seen as predating the baroque, unlike the relation in Deleuze, when, somehow, the baroque, or at least Leibniz, turns into the mannerist. Doubtless, we can never be precise about these periods. My own slender reading indicates that mannerism was a kind of formalization of Resnaissance naturalism, seeing painting is a matter of composing forms instead of reflecting nature. These forms could be arranged in meticulously complex ways and, apparently, sometimes distorted in a nonnaturalistic way. Michelangelo is a mannerist sculptor, apparently, with David seen as a formalised non natural figure certainly with a distorted body so that it looks natural when viewed from below.] Paper or cloth is folded in different manners, [deliberate styles?] and so are colours and sounds distributed. Apparently this leads to the idea that texture depends on 'strata that determine its "cohesion"' (41). It is different layers and their actions that produce the related qualities of the objectile. There are other factors affecting folding, including light and the effects of 'the hour and light of day' (41) [with a reference to some recent research—not properly referenced]. Depth has an influence, produced by the fold, as when paper is pleated to produce particular cards, or fabric is overlaid as in the work of Heinzen (below).  These qualities can sometimes be displayed in artistic forms such as Renonciat (below), where wood is sculptured to look like cloth.  Can a general notion of the material folds be developed, 'a spiritual point that envelops form' (42)? For Leibniz, 'primitive forces' in the soul were the origin of material folds, but these were always harmonized around the two levels. The paradigm, in this case referring to 'a model of the fold'. We have a number of folds' to choose from—the orient, or the Greek (below), are particularly important to Greek thought, a mixture of two terms, and an encirclement, the folding found in forms for Plato [and in some modern biology, it seems]. Clearly, these applied to different materials, but we're more interested in 'the formal element or form of expression'. This only appears when we start to discuss infinity and variable curves. The baroque fold then becomes 'the power of thinking and political force'. We can then proceed to produce formal deductions of the nature of the fold [something to do with the transition to mannerism again]. Folds are, like, jolly important. We can classify folds and deduce consequences from them, and produce agglomerations or conglomerations of matter [before that, apparently, we had to think about matter agglomerating through a form of weaving] Chapter four Sufficient reason [Finding Ch. 4 heavy going, I read Deleuze's online lectures on Leibniz first -- much more easy to follow! Lectures here, my notes here. Returing 10 days later, with more knowledge, greater confidence,and aching thumbs after doing DIY, while gathering my thoughts, I had several more attempts . This is a very technical chapter, detailing Leibniz's attempt to establish his own philosophical views against those of others. It is particularly difficult for me to follow these disputes because I have never studied philosophy. I am content to read in the lectures on Leibniz that, if the point is to defend the principle of sufficient reason ( and principles based on it) , this will require detailed argument about how predicates and events can actually come to be included in their subjects, since there seem to be several alternative conceptions. I'm going to go to the end of the chapter to establish the point that I think it is all aimed at developing: we have a unique trait that is found only in Leibniz's philosophy: the extreme taste for principles, far from favouring division into compartments, presides over the passage of beings, of thing and of concepts under all kinds of mobile partitions… There are two poles, one toward which all principles are folding themselves together, the other toward which they are all unfolding, in the opposite way, in distinguishing their zones. These two poles are: Everything is always the same thing, there is only one and the same Basis; and: Everything is distinguished by degree, everything differs by manner… No philosophy has ever pushed to such an extreme the affirmation of the one and same world, and of an infinite difference or variety in this world' (66). There is also a diagram (65) summarizing the classes of being and how they fit together so that we can apply Leibniz's principles to them.It also shows the proliferation of principles, which hre next chapter is going to argue is Leibniz's way of working, one which helps him avoid taking sides for or against more general and reductive approaches: 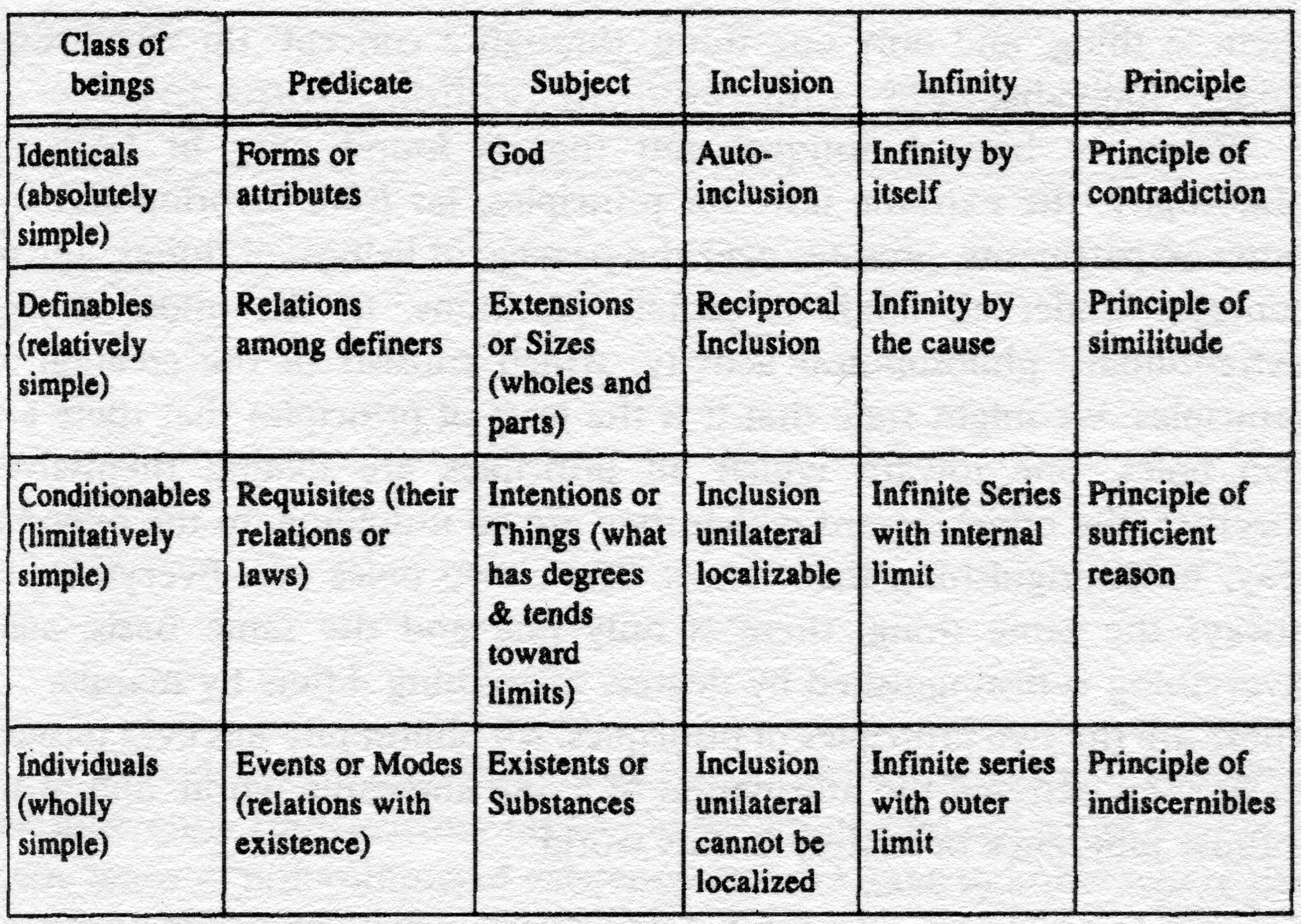 The columns seem to hang together in that to justify inclusions of different types of predicates in different types of subjects , you need different orders of infinity. The point of that is that inclusions of various kinds are central if sufficient reason is going to work across different applications. Real problems are involved here but they are mostly philosohical ones -making Leibniz's approach consistent,and addressing the claims and systems of other philosophers. As we go down the rows, we get closer to analyses of real existents. The first row is the classic approach most criticized by Leibniz ( although acknowledged) The second row down helps us develop applied mathematical analysis of Definables, something more tangible than Identicals, in relations that are like causes -- transformations or similtudes -- and here, Definables have become something more special -- Conditionables --which helps us get closer to concrete analysis . Then we get to the general form of sufficient reason, explaining things, and finally individual existents via the connected principle of indiscernibles. Some of these notions are unique to Leibniz, some he has developed with or against the work of others, as ever. Now to see if I can pick up any points in support...] [We might remind ourselves of the nice simple-- but pregnant -- statement in the lectures on Leibniz of the principle of sufficient reason, according to my notes, anyway: The principle means that 'whatever happens to a subject... everything that is said [truthfully] of a subject must be contained in the notion of the subject'. What is the notion? It is something also produced by reason—'reason is precisely the notion itself insofar as it contains all that happens to the corresponding subject'. -- no page numbers]The 'vulgar formulation' of the principle of sufficient reason is: '"Everything has a reason…"' (47). This results from 'the cry of Reason par excellence'. Causes are not the same as reasons, in that they only change a state of things, and they, like everything else, have a reason. We can call what happens to the thing 'an event', and these are included as predicates in 'the concept of the thing, or the notion'. We can go back to the earlier chapters about inflection, as something that happens to the line or the point, but go on from there to inclusion. Inclusion is a predication with inflection as the predicate, an 'other point that will be called metaphysical'. This is an example of what happens when we move from the event of the thing to grasping it as a predicate of the notion, a process akin to moving 'from "seeing" to "reading"'. We read the concept or notion in the thing itself. The concept 'resembles a signature or an enclosure'. The process of inclusion in this sense is crucial to sufficient reason—events become identical to predicates. It follows that everything must have a concept, or '"All predication is grounded in the nature of things"', and '" every predicate is in the subject"', where the subject means the nature of things, their notion or concept. This is a particular baroque notion of the concept, and Leibniz will use it to transform philosophy. It is a rejection of classical conceptions, including Descartes', where the concept is something logical, a generality: here it is metaphysical and individual. It is not defined by an attribute [something attributed to reality by thought?], but reality in the form of 'predicates-as-events'. However, there are different types of inclusion or analysis, truths of essence where the predicate is expressly included in the notion, and truths of existence, where predicates are a matter of contingency, something only 'implicit or virtual' [the lectures refer to these as inherent properties rather than essential ones]. Leibniz sometimes suggests that the former is finite, and the latter indefinite, but this is a misreading, especially since essences are 'inseparable from the infinity of God' (48). Conversely, analyzing existences introduces us to the infinity of the world, an existent infinity. We cannot have any indefinite elements in the world, since 'God would not be submitted to it', and it would also make it impossible to continue analysis. Further, Leibniz goes on to argue that we should see the implicit or virtual as not relating to inclusion of existents, but of essences [apparently, the term is applied to mathematical truths whether we are talking about 'intentional' or just 'stated' inclusion]. We can find a proposition of essence in all [purely logical] analysis, but not in 'propositions of existence'. We have to define what is meant by essence, although we have already implied a definition [in the mathematical examples?] An essence is when one term, the defined, is identical to 'at least two other terms (definers or reasons)' (49). The definition and the combination of definers can be substituted for each other, as in 'reciprocal inclusion'[the example is defining '3 by 2 and 1'—'and' here means 'add'?]. However, if we are to get at 'real or genetic definitions', only particular types of definition are used [we could define 3 as '8 minus 5...{but we choose instead}... the first {prime?} numbers that the defined includes and that include it']. We must also eliminate definitions that operate 'by genre and difference', avoiding extension, abstraction, and generality based on nominal definitions. We can use a chain of definitions, a 'concatenation of reciprocal inclusions' [as when we go on to add numbers as defined]. Finally, there is a philosophical problem to do with antecedents: on the one hand, the definers precede the defined 'since they determine its possibility', but on the other, they are the result of following 'the power' of the defined [potential? This term is used quite a lot, and I'm not always sure it is used consistently—in some cases it means the operation of multiplying a number by itself, as in raising 2 to the power of 3]: that is why we talk about reciprocal inclusion without adding any temporal dimension. Reciprocal inclusion also means that we can go back along the chain of definitions to arrive at 'undefinables... definers that are last reasons, and that can no longer be defined' (49). The process of going back cannot proceed indefinitely [towards the indefinite, material that cannot be defined], since we're working with real definitions—'the indefinite would furnish or have furnished only nominal definitions'. We now realize that the real definition cannot begin with undefinables [unlike other philosophers who try to follow this route from indefinables]. However, we do arrive at definitions that are 'absolutely first in the order of the before and after'—the '"simple primitive notions"'. We have to get to those to deal with endless indefinability again [lower down in the chains, as it were, where one term it is only defined by the one next to it and so on]. The simple notions have no reciprocal inclusions [they include other things but are not themselves included]: they are 'auto - inclusions'. Each includes itself and only itself, each is identical to itself [why do we have to add that? Because we need to make it consistent with the principle of identity? I think the argument is that we can then extend {'draw'} the notion of identity into infinity, 'without which identity would remain hypothetical ({as in} if A is, then A is A)'.]. There is a special, baroque conception involved, based on Leibniz's endless elaboration of principles. These are 'not universal empty forms; nor are they hypostases or emanations that might turn them into beings. But they are the determination of classes of beings' (50). We can see them as resulting from different classes of beings that are 'crying' [to draw attention to themselves]. At least the argument now indicates that we can use the principle of identity to become aware of things [through one of those inversions that we saw with the principle of sufficient reason. In effect we can ask that if A is A, in what sense is the second A included in the first?]. The argument leads to the 'Identicals, which are complete beings'. The principle of identity is not just abstract reasoning, but 'a signal' of the existence of Identicals: we would not necessarily know about them otherwise. Every form that is infinite is identical to itself, 'raised directly to infinity by itself and not by means of a cause'. These forms are '"nature susceptible to the last degree"', and it follows that they do not have parts, they are absolutes, also known as '"fundamental qualities", "distinctly knowable qualities"'. Because there have no parts, there can be 'strictly no relation with an other', including the impossibility of being contradicted. They are absolutely diverse, 'pure "disparities"'. In this sense, 'they surely form a category' [possibly meaning a category that does not rely on human thought?]. We can think of them as '"attributes" of God'. In this sense, Leibniz links with Spinoza in pursuing an ontological proof of the existence of God, unlike the shortcut that Descartes offers. By going through this detour, we've shown that it's possible to arrive at a real definition of an infinitely perfect being, without contradiction. The only distinction between the attributes is a formal one, not an ontological one, and God becomes 'both ontologically one and formally diverse' (51). We have combined—proved—that 'the totality of all possibilities...[is connected to]... the individuality of a necessary being' [represented by the symbol infinity divided by one]. To put this another way 'Identicals are a class of beings but a class with one sole member'[there is still a paradox of antecedence, however, since 'absolute forms precede God as do the first elements of his possibility, although God precedes them "in re" {in the matter of, in the thing} and "in actu" {in the very act, in reality} ']. But how do we move from the Identicals to the Definables? [And from mathematical equations and logical operations of reason to the real?]. Identicals can compose a unique being, at the metaphysical level at least. Definables however are 'derived notions', which can be relatively simple if they are towards the beginning of the chain of combinations, but which always have two primitives that define them in a vinculum [bond], sometimes defined by a [grammatical] particle. This process is the Combinatory, moving from primary to derived beings. There are three levels: level one where the primary or indefinable Identicals exist; level two where the simple derived beings exist; level three where composite derived beings exist, composed of three primaries, or perhaps a primary and a simple derived being.
We can see this 3-stage process in operation in mathematics. Here we have to construct relative primaries rather than absolute primaries. We might take prime numbers as primaries, or the fundamental axioms in geometry. From these we can derive a second level through the combination of primaries, than a third level [the example is taking the axiom as a definition of a point, the second level as combining the notion of a point with an intermediary space, so the third level is the notion of the line as connecting two points within an intermediary space]. In reality, God 'probably assures the passage from Identicals to Definables' (52). The point remains that it is difficult to explain how relations emerge, such as those demonstrated by 'articles, prepositions verbs and cases', in the passage from level two to level three. One answer involve some curious metaphysics about regions that accompany God and which are creative [produce reality]. This is found in baroque thinking as the notion of a 'several orders of infinity' [a horribly vague argument, this]. The second creative one operates with ['through'] causes that produce ['constitute'] wholes and parts, with no ultimate whole. These parts and wholes perform a series without a limit. The series develops through the 'principle of similitude or of homothesis' [an example of a transformation using similitude, as in the diagram below]. 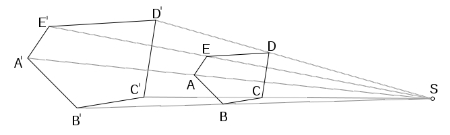 This is a new connection, not the same exactly as identity, but referring more to 'extensions or extensities', and not only of space, but also of time. This connection assigns a role to number, divisible matter, everything that can be subdivided into parts, which includes each term in the series. Given that this process is possible, if we have a whole, and a way of defining it in terms of parts, the parts can also take on the role of 'requisites ... reasons, or constituent elements' [the relation between requisites and causes is unclear --perhaps it is a matter of preserving the paradox of antecedence?]. We have in effect a numerical set, where a particular number can then be seen as a relation of other numbers, or a figure like a triangle can be seen as a requisite for a larger, more dilated triangle that we get by extending the sides in a regular way, as in the homothetic space. These operations and relations are related together [not just in the minds of mathematicians] because they reflect 'the original formula of a derived infinity' (53), and it is this that provides the intelligibility for mathematical relations. To push this idea, the primary terms do not have relations within themselves, but they have the possibility to develop them, they 'acquire relations' by taking on the role of requisites or definers of what is derived: they are 'the shapers of this material'. We considered the primaries first as simple bodies featuring auto-inclusion, and as the attributes of God, his predicates. But in this second infinity, they are no longer just attributes, and acquire a dynamic potential—they can 'become relations', and set up connections between wholes and parts. In this sense they are now reciprocally included with what they define. This is how we understand '"sufficient reason"'—the primaries are now the reason of the defined. We can consider the relations they display as 'the unity of the [original] nonrelation [absence of relations] with matters of [the ability to produce series of] wholes and parts'. Any apparent problems that Leibniz had with defining relations arose from considering attributes and predicates as the same. When we move away from the divine, and then to the second infinity, we find that derived forms have relations as their predicates, as in reciprocal inclusion. Apparently, even monads that have no parts, still have predicates, in this case '"affections and relations"'[they need these, in order to combine together in various ways?] There might even be a third order of infinity, characterized by a series that converges or tends to a limit [the mathematical definition of a limit is: 'the value that a function or sequence "approaches" as the input or index approaches some value' according to the Wikipedia entry]. Here we are talking not about extensions but intensions and intensities, and not relations but laws [I can't see why, unless what we are getting at here is that we can perform conventional and predictable mathematical operations on finite series? This might imply that we are dealing with some kind of stable reality?] We have not Combinatory qualities, but Characteristic ones [the characteristic might mean simply distinctive qualities, or, possibly: 'The least number of times the multiplicative identity in a ring needs to be added to itself to reach the additive identity' -- I think the slippage between common and mathematical terms assists the argument about connecting the mathematical and the real]. And here, the real emerges from matter in general, the thing, with 'inner characters' that determine magnitudes that converge to a limit. [Somehow] the relation between these limits is given by the differential,dy/dx [because curved forms are normal in Nature?]. What this means is that the differential equation is 'a law of Nature' (54). The notion of a requisite now refers to 'conditions, and limits, and differential relations among these limits'[that is to the relations that produce real things?] [complex and condensed argument here, and right at the crucial stage as well!]. We can replace the notion of parts and wholes by the degrees to which characters appear [the example is that the inner characters of a sound might include intensity, pitch, duration and timbre; the characters of gold include colour, weight, malleability and so on]. The real is not just matter in extension, but something impenetrable, displaying inertia [and also '"impetuosity and attachment"']: it has texture, provided by the 'sum of its inner qualities' and how they are related [in different physical states, for example?]. These new conceptions imply a third type of inclusion, a nonreciprocal or 'unilateral' one [because once it has been realized, a lump of gold does not turn back into its characters? A threshold has been crossed?]. In this case, sufficient reason turns into 'a principle' [to explain reality]: 'everything real is a subject whose predicate is a character put into a series'. These predicates are then added together to provide the limits of the series which real objects display. There are some interesting implications for knowledge. Our options for grasping reality are limited: once we move to the level of the third infinity, we have a different kind of essence—not intuitive essences, nor those produced by theorems. As a result, we cannot grasp them fully with mathematics. Real problems are distant from mathematical ones, and we are forced to deal with them by developing axioms which 'surely escape demonstration'. The notion of the characteristic in particular is 'a veritable calculus of problems or of limits': requisites and axioms are required to grasp problems, as conditions, but they are not classic Kantian 'conditions of experience', which means it is difficult to turn them into something universal. However, we cannot dispense with them. In fact, the terms we use as definers in arithmetic or geometry are really best understood as analogies to 'the inner characters of a presupposed domain' (55). Nor do demonstrations of mathematical procedures follows strictly syllogistic operations, but depend on '"enthymemes"'['informally stated syllogism{s} (a three-part deductive argument) as used in oratorical debates, often relying on premises that are probably rather than certainly true, or relying on unstated assumptions that are omitted because they are already well-known or agreed upon' -- Wikipedia again]. Yet characteristics and their combination are essential. We can try to understand inner characteristics from the outside, through experiments, for example. We can at least notice 'simple empirical consecutiveness' in animals. However, texture, 'the true connection of these characters… The intrinsic relations between the limits of their respective series' is more difficult, and requires us to display reason, or rational knowledge. We can apply this already to key elements such as definitions, and limits, demonstrations and even 'how enthymemes work for complete syllogisms'. However, there is still a problem connecting axioms to 'the order of necessary truths and demonstrations': Leibniz attempted at least to show that they revealed a form like that between wholes and parts. However, trying to establish characters leads downwards towards experiment and observations of animals, and upwards towards fully rational knowledge. To summarize, there are three types of inclusion: auto, reciprocal and unilateral. They feature in turn absolute symbols, Identicals; relative symbols, Definables; and requisites, converging series tending towards limits. The second type gives us the Combinatory, the third type the Characteristic. Using terms characteristic of the baroque and types of fabric, 'knowledge is known only where it is folded'. Chains of syllogisms and definitions can make up a fabric, but they have to be folded to become useful. Some ideas, found in the soul are so folded that we find it difficult to unfold or develop them. We can consider absolute forms like Identicals as 'simple and separated folds'; Definables are composite folds; requisites with limits 'resemble even more complex hems (and take up textures)' (56). Monads, with points of view, resemble draped forms. Monads are individual notions, not things but possible existants or substances. The term substance now completes the schema: 'identities, extensities, intensities, individualities; forms, magnitudes, things, substances'. We have already argued that the predicates of a notion, when it becomes a subject, form a convergent series tending towards a limit [eventually, passing through the different levels as above]. What this means is that we can work backwards from the individual in order to grasp the whole process, to comprehend or '"envelop"' the infinite. This is what monads do, in the opposite way, the inverse, to God. We can see the monad as the reciprocal of God (1 over infinity). Individual substances have requisites and inner characters, and this suggests a fourth kind of inclusion [some way below]. Leibniz 'salvages' Aristotle and says that the requisites of substance are found from form and matter, and active and passive powers. This makes the thing considerably different from substance. First, the thing has several internal characteristics, and thus can figure in several series [apparently connected by the differential relation again]. Because of this, we perceive things as a '"pleonasm"'['the use of more words or parts of words than is necessary for clear expression: examples are black darkness, or burning fire']. It is different with individuals: each monad expresses the entire world, even though it is only clear about one portion of the series [the example given is being clear about a pain, but not about the conditions that produced it]. However, the clear region of the monad overlaps with the clear region of another, prolonging convergent series into each other. This is where we get compossibility from. The world is made of all the series, and displays a kind of total curvature. The differential relation of that curvature now expresses the extension of one series into another [not just the relation between series as above]. There is also a fourth dimension to infinity, expressing a continuity that transforms all the series into a totality [an infinite totality which can also be called the 'transfinite']. It is no longer a case of a single notion producing a single subject, because monads can now express the entire world, although they differ in terms of how they do this. In this way, 'the principle of sufficient reason will become a principle of indiscernibles'[because monads overlap? ] The lectures discuss the principle of indiscernibles. My notes say: there can never be two absolutely identical things or that 'every difference is conceptual in the last instance'[that is, related to a concept we have of the thing?] The implications are delirious [no two drops of water can be identical, for example], and contradict classical logic, where the concept is general to encompass a lot of things. We can generalize, but if we analyze deeply enough, we will find that concepts relate to individual things only. This is the 'principle of indiscernibles'. If we take the second formulation, that every difference is conceptual, we only gain knowledge through concepts, the ratio cognoscendi, 'the reason as reason for knowing'. [The way the principle of sufficient reason 'becomes' the principle of indiscernibles, somehow all on its own, is a typical example of philosophical denominalization -- what it means is that Leibniz had to change it when allowing for individuals to square it up with what he thought about monads. These principles also show reciprocal argument -- who knows which one came first in Leibniz's thought, even though they appear as one following as a consequence of the other in the actual order of presentation?]. There is another difference. The texture of the monad must include a serial law affecting the deployment of its characters and 'the differential relation between limits', but the folds of the monad do not contain this law [I think this is arguing that the unique combination of characters and limits is not understood by the monad itself]. This is why the world is in the monad, but the monad itself must carry out its activities autonomously, as it were, although this activity is 'for the world'. This is how God understands individual notions. The overall law of the total world exists only at the transfinite level, not known to monads, even though they know, at some level, everything else. Only God chooses the world. This is Leibniz's 'cosmological proof of God's existence' (58). The monad contains the series, but not the reason for it, including the reason for its own particular role. Because monads never know the reason for the series, God must establish some preexisting harmony between them. This does not mean that the monad is necessarily impoverished: it establishes the force behind monadic activity. However, we have yet another kind of inclusion: the world is included in the monad but not localized there [or in mathematical terms, the limit of the series is outside the monad]. So we now have four kinds of inclusions to correspond with the four infinities: 'the infinite sum of primitive forms (= God); infinite theories without limits; infinite series with intrinsic limits; infinite series with extrinsic limits that restore an infinite whole (= World)'. We can now solve some apparent ambiguities in Leibniz, turning on the different sorts of essence that he operates with: one [logical, mathematical] kind seems to lead back to the Identicals, but the truths of existence seemingly cannot be reduced to identical truths, and involve infinite analysis. We can always stop the chain of definitions if we wish, and use one as if it were an identical or requisite, at least in the domains of logic and matters: we cannot do this when looking at truths of existence, however [why not? This is so operationalism proceeds]. Nor is the analysis of existents easily seen as virtual as opposed to actual analyses of essence [I would have seen this is the other way around]. However, it all turns on different notions of infinity and inclusion. Technically, all analysis is infinite, but there are different types. Even the notion of existents implies that the whole world is still included [as in the causes and effects of Adam sinning etc] , so that 'virtual' comes to mean 'current inclusion that cannot be localized' (59), and this is like some aspects of essence. This means that the world is a first in a virtual sense, but the monad is first in an actual sense. When discussing the Requisites, the virtual means something else again, relating to the unilateral character of inclusion. Leibniz's example here turns on the sort of inclusion where the sextuple is included in multiplications of 12 mentioned above, but there are other examples where it is not so easy to extract elements that are included, as in deriving values for square roots, or dealing with differential relations where the quantities might not be on the same numerical base. The real distinction is between cases of inclusion [not those other traditional terms like virtual and actual, essence and existence]. The mathematical exercises like extracting square roots or finding a way to relate quantities as ratios shows us how to analyze things as a determination of predicates, considered as requisites. Actually existing things, existents, involve considering a series of powers with extrinsic limits. However, there is still 'an incertitude that is objective'. Is the fundamental relation ['the fold'] one between essences and existents, between 'the essences of God and what follows? Or between the essences of things and existents?'[The last one is the one that interests me in particular—how does reality come out of a series of forces and curves?]. Predicates are only attributes when we are talking about infinite forms and notions of God, and because we'll never know about God for certain, they can only be rendered as 'conditions of possibility for the notion of God'. In all other cases the predicate has a relation or an event (we can see relations as types of events), and we can now apply mathematics to understand them. We can also consider events as types of relations, relating to existents and to time. Particular events or relations, verbs or prepositions, turn notions into subjects, and this is quite a different process from attribution, to Descartes attributing being a thing that thinks to the thinking subject, for example [and presumably this is also different from Spinoza?]. Leibniz relates subjects, verbs and objects in a 'baroque grammar' (60), where the predicate is a relation and an event, not an attribute. Predicates are separate acts, movements, change, expressed in the proposition itself as emergent, not reducible back to the subject. When we think, we need to analyse this passage from subject to object, instead of thinking in terms of permanent attributes of the subject. This is what lies behind the notion of the event. The event is worthy of analysis in itself, and requires a separate concept. The Stoics [whom Deleuze much admires, and he has used this example elsewhere], saw the event as the incorporeal part of the subject, so that trees are not green, but rather '"the tree greens"'. Propositions therefore state 'a "manner of being of the thing"', or 'an aspect' (61). For Leibniz, the world itself is an event, something incorporeal or virtual, and therefore must also be included in every subject, but this time as a basis to understand the point of view of the subject [and the 'manners' which correspond to this point of view—I think 'manners' here means modes of perception]. Manners are particular predicates; the world is 'predication itself'; the subject goes from one particular predicate to another, one aspect of the world to another. This helps us replace notions of form or essence with the terms basis and manners. Certainly, mannerism is opposed to essentialism, and the baroque notion is inherited from the Stoics. There are sometimes difficulties in actually extracting these terms, for example when the predicate is not actually stated in the sentence, or if a subject is missing [the examples are sentences like 'Here are three men', where three appears to be the subject, or at least refers to some extension of a human subject. Similarly, to say that 'water boils at 100°' has a subject, water, a thing, but the predicate implies 'a vaporisation curve' at a particular value]. Similar problems relate to statements of size, which can refer to subjects, extensions of the subject or predicates of the thing. Overall, what Leibniz offers is 'an entire history of the concept', progressing through notions of wholes and parts, things and substances, and incorporating 'extensions, intensions and individuals'. At each level, the concept itself can become a subject. This is quite different from classical conceptions which saw the concept as the being of reason, an essence or logical possibility. In Leibniz, it has a metaphysical reality by being attached to a corresponding subject. Classical logic is also challenged because predicates are no longer attributes, but are internal relations [which have to be analyzed and cannot simply be deduced or posited?] We see the implications in the theory of substance. Nominally substance is 'concrete, determined, individual'(62). But it is also 'subject to inherence or inclusion', supposedly with internal elements [including those that produce events]. However, classically, these characteristics were replaced by the notion of the essence or attribute, so that these internal elements are not there by accident, and thought requires individuals to display 'modes of the attribute as it generally is' [in Descartes]. Individuality disappears. For Descartes, substances were simple notions, and their elements needs to be abstracted through the application of reason. For Leibniz, simplicity needs to be rethought: there are many simple notions that lacked substance [an example?]. Leibniz prefers to talk about simple substances combined into composite ones not through reason but through metaphysics [nonsubjective processes], invoking a notion of 'a unity of being'—this might lead to problems specifying particular modes of being, but Leibniz refers to 'degrees of unity'[this might also lead to subsequent problems with having to posit some universal substance, the vinculum substantiale—see notes]. Substance is unified in such a way as to produce movement and change, something more than simple extension. We often do not see the inner unity behind accomplished movements, but all movement refers to a process between the unity displayed in the different instances, and also a inner unity 'for the totality of its duration'(63) [this apparently is 'the physical criterion of substance']. There is even a kind of 'active unity' that incites movement while preserving totality [this is the 'psychological criterion' of substance, referring to 'perception and appetite']. So substance shows us movement as event and change as predicate. The logical criterion of substance is inclusion, the inner unity of subject and predication, but not as attributes. Descartes also screwed up by comparing the simple to the complete, in order to develop the notion of real distinction, but the latter also 'entails only the concept' in the first place. What is entire, the sum of what belongs to the thing, is supposed to define what makes the thing really distinct, compared to other things. However, this confuses the distinct and the separable, for Leibniz. The issue turns on requisites, which all beings and substances possess. Requisites are what constitute substance, through five criteria: 'metaphysical, unity of being; logical, inclusion of the predicate in the subject; physical, inner unity in movement; psychological, active unity of change; epistemological, the requisites of inseparability'[the last one seems to turn on an argument that ultimately, nothing is clearly separable, and several substances might have common requisites] None of these involve essences. Unlike classic thought, which 'needs a solid and constant attribute for substance', Leibniz tends towards the mannerist, where 'the spontaneity of manners replaces the essentiality of the attribute' (64). Aspects are connected as a series, not through abstractions, there are complex movements. There are also complex thoughts or experiences, where different perceptions have been connected together to produce some overall feeling like anxiety, as in 'the universal anxiety of the animals watching out for danger... [that leads them to]... grasp the imperceptible signs of what can turn its pleasure into pain'. The sensation is assigned by the soul [a version of how apperception emerges from perceptions?]. This lies in the depths of the soul, and these omnipresent depths are also a feature of mannerism, because they blur the clarity of the form, which is what produces spontaneous manners in the first place. Some commentators see the work as 'the play of principles within principles'[emphasis on the play for me, and the logic that works in both directions to make things consistent]. The terms are 'slippery' and cannot easily be pigeonholed. Rather, 'they reign by unfolding themselves in a zone', and are folded into that which precedes and follows them. But this is consistent with the notion of sufficient reason and its explication in the principle of indiscernibles, for example. Sufficient reason used to be confined to the zone of similitude and definables. Contradiction used to be seen as something separate, but we can now see it as a part of 'the very reason of the Identicals' (65) [because the Identicals are not in contradiction? I'll have to go back and check that bit]. Indeed, when discussing Identicals, 'non contradiction suffices as reason' and [more bafflingly] 'the principle of contradiction is a case of sufficient reason'[a note refers us to Leibniz himself, and his apparent view that sufficient reason should also be extended to examine contingent truths as well as necessary ones]. In the actual work by Leibniz, there are lots more principles and transformations of them. They include arguments that 'sufficient reason is the reciprocal of non contradiction', or that 'the principle of indiscernibles is also the inverse of the principle of sufficient reason'[turning on arguing that we perceive a concept through a thing, and also a thing and only one thing through a concept]. This is the extreme taste for principles, avoiding compartmentalization, examining the passage of things, leading to the two poles... Chapter five Incompossibility, individuality, liberty. Adam sinned, but he could have not sinned— there is no inherent contradiction between the two states, although there may be between the two statements, and this applies to all the existents [contradiction is possible with logical statements]. The issue turns on the world in which Adam sinned leaving no room for Adam not sinning, although Adam not sinning would be possible in another world. The two worlds are related not through contradiction but vice-diction. Deleuze explains what follows from this concept for him in a lecture: We should call vice- diction this quite different procedure to contradiction. It consists in traversing the Idea as a multiplicity. The question is no longer of knowing whether the Idea is one or multiple, or even both at the same time. “Multiplicity”, used substantively, designates a domain where the Idea, of its own accord, is much closer to the accident than to the abstract essence, and can only be determined with the questions who? how? how much? where and when? in what case? – all forms which trace its true spatio-temporal coordinates. A discussion also appears in Difference and Repetition ( according to my notes): Leibniz starts with the ‘inessential so far as phenomena are concerned, with movements, inequality and difference’ (56). This involves seeing otherness as a property, not an essence, expressed in cases. The procedure which links cases to the essential has a special name –‘vice-diction’ as opposed to contradiction [several online commentaries argue that vice-diction is what Deleuze calls countereffectuation or counteractualization in LofS—one examines concrete cases in order to trace the operation of the virtual. Here it is a bit more obscure—contradiction operates with properties that are contained in the essence, to gloss this quite a lot, whereas vice-diction sees the relevant properties in the case, not in the essence. For our purposes, the issue is that the possible worlds are linked through the notion of incompossibility. We cannot know the real reasons for god creating all these worlds, but we can 'demonstrate that he possesses some of them, and what their principle may be'[exactly how the mathematics works, says Deleuze] (68). The world is 'an infinity of converging series', turning around unique points. Every individual monad expresses a part of this world, a finite sequence or series. However, the series can diverge 'in the neighbourhood of' singularities, and this will produce another finite world. The worlds are compossible because they are part of the totality of converging and extensive series, and the totality of monads. The incompossibles arise when the series diverge, and the monads express the differences [there is a {composite} monad Adam the nonsinner]. There is no underlying absolute world behind these differences: our world is relative but it is the best, 'the one that has the most possible reality'. The principle of the best allies with Leibniz's other principles to further develop the notion of sufficient reason [ I am sure I could work out exactly how if I had time] . God first creates worlds and all the individuals in them, as 'a series of inflections or events: it is a pure emission of singularities'. The singularities include being the first man, living in a garden of paradise, having a wife created from your rib, and sinning. The singular events have related ordinary events, which surround them as 'a cloud'. In fact there is a connection between ordinary and singular points if singular points arise from the connection of two ordinary ones in different vectors [as in the corners of the square]. In the abstract, everything is ordinary ['regular'] and/or everything is singular, but we have to distinguish them in particular cases and 'on a given scale'. The four singularities attached to Adam, above, are extended along regular lines 'that have common values in both directions' (69). If a fifth singularity appears—resistance to temptation—it doesn't exactly contradicts the other, but rather appears as a choice, because it does not pass through the same common values—'it is neither the same garden nor the same primeval world'. We may not know the reason for this divergence, but we can at least use it to explain why Adam the nonsinner cannot appear in this world. This is another example of 'a calculus and even a divine play', and Leibniz was the first to see it as 'a calculus of infinite series ruled by convergences and divergences' Leibniz's Theodicy offers a typical baroque narrative, with one story enclosed in another, but it is a philosophical dialogue [about mythical characters, including Theodorus who has his dream of reality as a pyramid with worlds at each level—see lectures]. Apparently, a particular character, Sextus, appears in each compartment with a number on his forehead, referring to a page in a book found at each level, describing the world at each level—'the baroque combination of what we read and what we see' (70). The series diverge at the point at which one of the characters leaves the temple. Similar ideas are found in Borges [another repeated example] with his story of the baroque labyrinth where all possibilities are laid out in the form of parts through a garden. There is another novel by LeBlanc, also inspired by Leibniz, based on the incompossible interpretation of three singularities [signs including a tattoo and some fingerprints], which spells out the different possibilities which might explain the connection and its meaning. These developed Leibniz in a particular way by keeping all incompossible worlds in existence at the same time, but this would make God into 'a trickster' (71): Leibniz says that we can understand the rules of His game, however, to establish why one possible world exists. This leads to a discussion on individuality. Monads convey the world through one partial zone or subdivision according to its point of view. Every actual human individual can experience these partial zones in their bodies as monads pass through them. We can develop this by saying that an individual can be understood as a number of local singularities which serve as '"primary predicates"': the four above are the primary predicates of Adam. An individual is produced by 'concentration, accumulation, coincidence of a certain number of converging preindividual singularities' (72) [so this is where the insistence on preindividual components, in, for example, Logic of Sense, comes from]. The preindividual characteristics can also be shared with other monads - -hence the overlaps with compossible monads. The monad has a nucleus or kernel, and it is composite, not a simple notion. We have to depart from Leibniz [to not pursue the path into the infinite?] to argue that these predicates are requisites for the individual, a 'real [not just a formal] definition'. This explains why each individual expresses only part of the world—the singularities determine the particular region it can express. However, the singularities also extend in all directions, so each individual can express the whole compossible world. God creates many Adams sub ratione possibilitatis ['the notion is exactly what it would be if the individual existed,but the existence is merely possible, and is not, in the mere notion, judged to be actual' according to Russell, B. (2013) A Critical Exposition of the Philosophy of Leibniz. Cambridge: Cambridge University Press, via Googlebooks].Singularities are given proper names, like Adam, to indicate that they can be isolated, becoming indefinite, something that can be considered sub ratione generalitatis 'in general terms, in terms of an essence or of a specific or incomplete concept' (Rutherford, D. (1998). Leibniz and the Rational Order of Nature, Google book), so that the subject becomes an Adam in general. In any event, individuation is not a matter of going from a [general] genre to a [more specific] species, for example but going 'from singularity to singularity', governed by convergence or prolongation. The individual is not defined by being a member of the species. Only individuals exist, or but they do so 'by virtue of the power of the concept… to become a subject… condensing and… prolonging singularities' (73). Singularities are events or 'droplets of an event', and preexist individuals. Individuals are best seen, therefore as 'the actualizations of preindividual singularities'. Any attempt to discover any other forms of determination of individuality already presupposes this individuation. In mathematics, the individual thing does belong to different species ['is necessarily specific'], because they alone can be specified as involving a relation between to definer [the example is the relation of axes to produce an ellipse]. But with physical or organic things it is different. Different characters produce series, which never stop 'varying or dividing'. This produces 'multidetermination', but all this lies within this series, not with external forces [we're getting close to the differences between differenTiation and differenCiation in Difference and Repetition]. In Leibniz's terms, what individuates the body is the soul, but the soul is inseparable, and not external. Likewise, all substantial forms are within the thing. Only once we assume this process, and its result in producing the individuated, can we talk about determination from the outside. This relates the principle of indiscernibles and the law of continuity. The law applies in the 'mathematical domain of wholes and parts, the physical domain of species or corporeal characters, the cosmological domain of singularities and the way they are extended' (74). The principle argues that no two similar individuals can be distinguished solely from the outside: the soul specifies the singularities that will be used to produce the individual, and it then individuates bodies compared to species. Species are themselves individuating, because two figures of the same species, even if they are physically different, can refer to the same '"soul or entelechia"'[I think this is saying is that the similarities of the soul outweigh any physical differences] In other words, the existence of individuals should not be seen as gaps in continuity. Instead, they are rational divisions of continuity, leaving no holes [because they can still link up]. There is no suggestion that the difference between individuals is internal and irreducible [the wrong way to read indiscernibility], or that it converges to zero [the wrong way to read continuity]. Continuity makes the values attached to the terms of the relation to vanish, while preserving its 'inner reason'[just as the differential preserves the difference even when X and Y are at zero]. This is consistent with Leibniz arguing that polygons become circles, the rest is a part of movement and so on. The important differences are 'intrinsic, intelligible or conceptual' (75). The most general example of continuity is found in the concept, which presents us with not knowing 'where the sensible ends and the intelligible begins'[implying that the sensible and the intelligible coexist]. We also find continuity in the monad, or the soul: when we examine how individuals extended by singularities, they never actually fully reach neighbouring singularities, but taper out in the form of infinite subdivisions—'favoured zones that belong to each monad'. These zones account for the various traits of the monad ['vegetal, animal, human, or angelic'], or its 'degrees'. [A way of preserving maximal connections between individuals, while retaining borders between them?]. So to summarize, the world emits singularities, organizes them in series, 'invents rules of convergence and divergence'so that the series produce infinite totalities, and make these totalities compossible or incompossible. Singularities are allocated to the nucleus of the monad or the individual which can then express a compossible world. God is ultimately responsible for choosing the best of these organisations and allocations. Ultimately, this will help us understand actualization in individuals, and the realization of matter. We can return to architecture to discuss the 'tastefulness' of the building, the number and elegance of the rooms, and the convenience and 'rightness' of the grounds, materials and facades (76). This is the play of architecture, and the game is to fill a space with the fewest possible voids and the greatest possible number of figures. This helps us to see space and time as offering 'an order of indivisible distances from one singularity to another or from one individual to another', or as a continuous prolongation. These understandings produce 'the board on which the game is played and the material of that board'. This gets us to the notion of the world as throwing the dice, which in Nietzsche and Mallarmé involves introducing contingency, without principles, making the world anonymous, an apparition, covering nothingness. This nihilist phase followed the collapse of theological reason. Baroque philosophers were interested in trying to hang on to the theological ideal to stop a total collapse, even though there were increasing challenges. 'The baroque solution is the following: we shall multiply principles… and in this way we will change their use'. The point now is to find the principles that are explained in particular objects, especially puzzling ones—'the case being given, we shall invent its principle' (77), which is 'a transformation from Law to universal Jurisprudence'. Bringing God in as the one who chooses the best is a defensive tactic to try and save the notion of the Good. The real game is one involving excess of principles, inventing principles, a' game of reflection', 'a game of filling holes' to stave off nothingness [finding sufficient reason everywhere]. Opponents are encircled, made incompossible, made to exhibit divergence. In this sense, the baroque is the last flourishing before the world lost its principles, a final 'hubris of principles'. In this way, Leibniz rescues God, but only in a diminished way, compared to the old conception. It also seems to lead to a fatalism, once you have accepted the world is the best. The philosopher therefore does not interrogate or judge reality but becomes 'a Lawyer, or God's Attorney' (78), and this gives us the meaning of 'theodicy', [apparently a word that Leibniz invented]. The old order has collapsed, and now has to be built again using new principles, defended in all its detail on the basis of those principles. This is 'a schizophrenic reconstruction', something that follows from modifications within, within monads in this case. Their actions can be seen as taking part in a baroque dance, 'in which the dancers are automata', a matter of postures [which can be seen as an aspect of mannerism]. The liberty of God is preserved, even if it is only to choose, and human liberty can also be related to choice. We have seen that alternative choices, for Adam or Caesar, are not impossible, but they are incompossible with the chosen world. This limits the idea of tight necessity for action, but does not exactly safeguard human liberty, because it is always practised in this world. This does not leave much room for human action, which 'remains in a condition of closure'. Incompossibility does not guarantee voluntary events, or free will—human beings are suffused with schizophrenic automata. It looks like we are arguing that attributes of the human being do not include personal liberty, but Leibniz replaces the attributes with predicates, events, and these can appear to subjects as 'a change of perception'(79), which does allow a certain freedom again, because we can find their reason for a change of perception, which might include a motive. Leibniz therefore develops 'the first great phenomenology of motives'. He says we must not objectify them as if they were the factors that could be weighed or assessed, with action as a kind of resulting vector. We must not divide [prioritize?] motives either: if we are really to choose motives, there must be 'an infinity of subjective motives' in the first place. Anyway, the soul invents its own motives, so in that sense they are always subjective. Motives arise from an accumulation of minute 'inclinations', that together produce a state of disquiet or anxiety. This produces a change of amplitude in the soul, so that it bends in a particular direction. [The example refers to the number of minute choices required in order to choose between staying home or going out to a nightclub]. The action itself has effects, once the amplitude of the soul is affected in the first place. Voluntary acts are free in the sense that 'they express the entire soul at a given moment of its duration' (80), and thus expresses the self. Other amplitude and other directions are possible, and it is our job to examine the factors involved for ourselves. So: inflections are included in souls. We can now consider inclination as 'the fold in the soul, inflection the way the fold is included'. The soul features inclinations, but not determinations. Inclinations arise in the present not the past, but the past contains an infinity of living presents, so in this sense, an act summarizes the past and anticipates all the effects, to infinity and both directions. The present is privileged because it is inherent in the monad, a part of a unified movement. [It looks like this unity arises because predicates are given verbal value—at least in humans?] This inherent quality becomes 'the condition of liberty and not of impediment' [monads have determined characteristics, but some of them permit them to be free, at least in this limited sense]. All acts involve motives in this way [?], so they can all [the perfect or completed ones anyway] be considered as entelechia [entelechy is defined as '1. In the philosophy of Aristotle, the condition of a thing whose essence is fully realized; actuality. 2. In some philosophical systems, a vital force that directs an organism toward self-fulfillment' (The Free Dictionary)]. With his concept of a unity of present and past, Leibniz resembles Bergson, although again there is no determinism, not even an internal one: on the contrary, the internal dimension guarantees liberty. Although it is grounded in a particular zone of the monad the present can be extended and also varied in intensity, as in different 'amplitudes' of the soul. Even Adam is capable of not sinning, but that would have required his soul to have taken another amplitude, and unified another movement. It is this total potential which makes acts free. [An example follows discussing damnation as consequence of a persistent hatred of God, not of a particular act in the past. The damned have shrunken souls with only one predicate—hating god. If you can open the soul again, you will cease to be damned, so even the damned are free in the present. There is a connection with narrow and obsessional ressentiment in Nietzsche.]. So it's possible to amplify the soul in a different direction, or to pursue another fold or inclination. Although this is fully possible only in another world, the very restraint of this world shows this possibility, that the soul could, in principle any way, do something else [a very abstract notion of liberty]. The issue turns eventually on whether or not we are too lazy and narrow minded to modify our own souls, even though God has inscribed them in their basic form. In the end, we should focus on 'actualizing the liberty of a given soul in this world' (82). The [normal] automaton is programmed for mechanical actions, but 'the "spiritual automaton" is programmed by motivation for voluntary acts'. [Again there are similarities with Bergson, on the unity of past and present in the act but, in Leibniz, only God makes future acts necessary, because he is a supreme reader, the only one who can '"unfold all the pleats that are only sensorially developed over time"'[citing Leibniz]. Here, the notion of predestination looks like determinism again. It is not that God knows absolutely everything in advance: rather he is always present, in all the conditions of the monad, as a kind of natural force, which helps him to read the activity going on in the monad to unify past and present [this might help later thinkers, like Whitehead, unifying natural forces with human ones?]. Divine eternity in this sense means being present in all the passages going on in present living beings. There is a [small] space for liberty, then, but not morality [in the sense of a 'general tendency to the best' (83)]. For Leibniz, it is a matter of extending the amplitude of a reasonable soul, and the opportunities to do so are going to vary, for example between children and adults, the sick and the well. So this is going to be very individual and concrete, but we must do our best to 'produce a free act that expresses the most possible in one given condition or another' [it seems to be rather like the notion of ethics of joy in Spinoza, where we seek out experiences that expand our selves and avoid those that diminish them]. In this way, we bring about progress, as we experience of the consequences of our choices [described rather grandly as 'prolonging God's passage to the maximum, actualizing all the singularities that are concentrated on, and even won over to, new singularities' (84)]. It is a matter of amplification or intensification as well as just extension. However, this might work for individuals, but how does it add up to 'the total quantity of progress'? This would require all the monads to converge, to become simultaneously reasonable. But not all souls are 'fated to become reasonable', or at least not all at the same time. First they have to be switched on [rendered as 'a flame lit within the dark monad']. Also, they die, 'fold infinitely upon ourselves; we return to the state of the animal until the bodily resurrection'. It is important that we get our last thought right, make it as reasonable as possible, and not narrowed, especially not narrowed as the damned do, dying consumed with hate. Sequences of birth, activity and death affect all notions of progress. When 'the monad is summoned to "live" —yet more when it is called to reason—it unfolds in itself this region of the world that corresponds to its enclosed enlightened zone'. However, not all are called. Some souls remain folded. Others have fallen and folded into themselves, others are damned 'hardened in a single fold that it will not unfurl'(85). These are the possibilities, and the soul can enter the first one, an area of 'development, of distinction, and reflection',and thus escape the normal statistical variations within it. Only the damned suffer any detriment from others progressing. The infinity of the damned even guarantees ['founds'] the best of all possible worlds, because 'they liberate an infinite quantity of possible progress' [there is some zero sum game involved in total progress?]. Again we can think of the damned as occupying the lower floor of the baroque house, with the saved above it, as in the painting of the last judgement. [A curious discussion of the zero sum game to end this chapter—'God does not determine the total quantity of progress... [except]... eternally, in the calculus of the infinite series that moves through all increased magnitudes of consciousness and all the subtractions of the damned'(85)] Chapter six What is an Event? [This is a quick aside comparing Leibniz with Whitehead: the real issue is the one we've seen above whether chaos is ordered as a chaosmos. Stenner has a good article on Whitehead, as above, and this chunk of definition also helps: For example, the word “prehension,” which Whitehead defines as “uncognitive apprehension” (SMW 69) makes its first systematic appearance in Whitehead’s writings as he refines and develops the kinds and layers of relational connections between people and the surrounding world. .. these relations are not always or exclusively knowledge based, yet they are a form of “grasping” of aspects of the world. Our connection to the world begins with a “pre-epistemic” prehension of it, from which the process of abstraction is able to distill valid knowledge of the world. But that knowledge is abstract and only significant of the world; it does not stand in any simple one-to-one relation with the world. In particular, this pre-epistemic grasp of the world is the source of our quasi- a priori knowledge of space which enables us to know of those uniformities that make cosmological measurements, and the general conduct of science, possible.(Internet Encyclopedia of Philosophy) ] Whitehead is another philosopher that asks what an event is, and in the process, criticizes the notion of attribution, but also the proliferation of principles, and the conceptions of the subject. He is the last proper Anglo philosopher 'before Wittgenstein's disciples spread their misty confusion, sufficiency, and terror'(86). Events can be something that has just happened, but also something that has lasted for ages, as in the Great Pyramid. Such lengthy passages of duration raise issues of the connections with Nature or God. We can see events as produced from chaos, via a screen, a transition from the many, 'disjunctive diversity', to the One, meaning in this case 'a certain singularity'. The screen acts something like a membrane or an electromagnetic field, and it filters chaos to make something. In Leibniz's terms, chaos would be the many possibilities, while the screen would select only the best of compossibles. In another metaphor, chaos can be seen as depthless shadows, while the screen offers a more conventional black composed of all the colours [a reference here to dark backgrounds in baroque paintings, the fuscum subnigrum]. In another metaphor, chaos is 'universal giddiness, the sum of all possible perceptions'(87), and the screen extracts differentials that will permit ordered perceptions. It could be that chaos itself is a function of the ability to perceive the operations of the screen. So for both Whitehead and Leibniz, the event involves extension, as stretching, the creation of a whole by combining sequential parts into an infinite series [the ends of which may be beyond human perception]. The event is also 'a vibration with an infinity of harmonics or submultiples', whether sonic or visual. We can see space and time as 'abstract coordinates of all series, that are themselves in extension'. Extensive series have intrinsic properties as well—'for example, height, intensity, timbre of a sound, a tint, a value, or saturation of colour'- and these take up finite series or conjunctions. Overall, matter, 'what fills space and time' has a texture produced by the different materials in it, which are not only extensive qualities but intensive ones, 'intensities, or degrees'. The texture produces something definite, 'this rather than that' (88). Whitehead arrived at these conclusions from mathematics and physics, although they coincide with those of Leibniz. The individual is the third component, and here there are differences. Whitehead sees the individual as creativity, something personal, concrete, composed of 'a "concrescence" of elements'. It is not just a passive conjunction, but a prehension, that produces individual unity. Prehensions grasp elements that are themselves prehensions, and so we can eventually end with a prehended world. Living beings prehend inorganic material. The pyramid can prehend people watching it. Prehensions anticipate full human subjectivity, as prehending subjects become superjects [see above]. There is also a shift from private prehensions to public ones [as when prehensions become data in public discourses?], but we have to remember that the datum is itself a prehension. We're talking about a process of objectification that is also subject to subsequent subjectification. Events can be seen as 'a nexus of prehensions' [are also unified by the activity of prehension?], and therefore multiple, 'at once public and private, potential and real, participating in the becoming of another event and the subject of its own becoming'. Prehension has other characteristics. The subjective form is necessary as a way in which the datum expresses itself, or the subject actively experiences it [the examples include 'emotion, evaluation, project and conscience']. In other words, the datum folds itself into the subject through a subjective form, a 'feeling' for Whitehead, or a manner. There can also be negative prehensions that which involve excluding data from the nexus. Subjective aims produce a passage from one datum to another, or from one prehension to another, 'in a becoming'(89), and the past can also be united with a present and an anticipated future. Finally, there is self enjoyment or satisfaction [rather like an increase in joy], where subjects experience a richer private life, and where 'prehension is filled with its own data'. There is a Christian notion of being filled with the Glory of god, and 'the self enjoyment of... [our]... own becoming'. We find all these in Leibniz's monad. Perception is the datum of the prehending subject, as in point of view. But active perception can take other forms, for example 'sensitive, active, or conceptual', and these forms make up distinctive ways or manners in the monad. The movement from one perception to another is described as appetite, and appetite is required for becoming. Becoming also involves pleasurable integration which fills the monad 'when it expresses the world'[like being able to enjoy music without necessarily calculating its harmonics]. The issue tends to focus, for Leibniz, Whitehead and Bergson, on explaining something new in an objective world, accounting for 'a subjective production of novelty'. In the best of all possible worlds, and only private subjectivity was available, except for the damned. Nevertheless, private subjectivity could be creative and innovative in 'a teleological conversion of philosophy'. For Whitehead, we have to first consider the notion of eternal objects, the last in the series extension, intensity, individuals and finally eternal objects or '"ingressions"'(90). The first three are constantly moving and flowing, and so are permanent objects originally—they still 'constantly gain.. and los[e] molecules', but also remain the same: they can be considered as pure possibilities and also pure virtualities that are actualized in [by?] prehensions. They are the result of apprehension [a synthesis, 'conceptual feeling']. [This is never purely subjective though and] sometimes ingressions are the result of particular qualities which combine prehensions ['qualify' them]. They can also arise through Figures 'that determine an extension', and Things 'that cut through a matter'. So they are not separated completely from flow or from creativity, but arise from a process of actualization or realization that set limits to the flow. Prehensions can actualize. It is a matter of ending the process of incarnation: for new things, it is more a matter of finding the conditions [of emergence]. For Leibniz, the monads actualize virtualities in themselves, and also realize possibilities in composite subjects [qualities], aggregate materials [things], or extended phenomena [figures]. There is a constant flux with solids emerging and disappearing. Monads actualize, but their reflections also produce possibilities that can then be 'born in the extended composite materials'. 'Figures, things and qualities are schema of permanence that are reflected or actualised in monads, but that are realized in flux' (91). If we take the example of the musical concert, we can see it as a matter of vibrations of sound dispersing through space, developing harmonics and submultiples. The qualities of the sound include height, timbre and intensity. The sources of the sound, 'instrumental or vocal' (91) interact among themselves, responding to what another source has developed. At this stage, Whitehead and Leibniz would be in agreement—the monads or prehensions are filling up their perceptions and moving to other perceptions, relating to the notes of the scale as 'eternal objects', both in terms of actualizing virtualities, and realizing possibilities by turning them into vibrations or flux. However, for Leibniz, there are additional considerations relating to the baroque, in that the concert can be seen as two sources of sound, self contained, but in harmony: harmonies 'replace horizontal connections' between these two subdivisions. This would be quite different from Whitehead, who sees prehensions as being directly connected to each other, taking each other as data, and forming an entire world, except those that are negative prehensions and are excluded. It is the same world. For Leibniz, it is a compossible world, where incompossibles have been excluded. Monads have no direct contact with the world outside themselves, no horizontal relations, no 'intra worldly connections', but a harmonic relation, where they can express one another without any direct contact. In neither case do the monads or prehensive units have sense organs, doors or windows. For Leibniz that is because the world is already closed [tightly defined] by compossibility, but for Whitehead, the world is open so that all prehensions exist only as prehensions for another prehension, which either include or excludes it. 'Prehension is naturally open… onto the world' (92). For Leibniz, divergent series should be seen as the borders between incompossible worlds. For Whitehead, divergences of all kinds, incompossibilities and discords all belong to the same world. This diversity cannot be expressed, but it can be grasped through prehensive units and the 'variable configurations or changing captures' that they develop. This is Whitehead's view of chaos, or chaosmos, not even regulated by the choices of God. God instead becomes simply Process, that affirms even the incompossible. Indeed, divergence becomes central to the world. All that can be achieved, by monads, or by modern mathematics, is a series of captures, 'syntheses associated with each path'. This confirms the notion of the baroque as 'a transition', perceiving classical reason as unable to tolerate the increasing impact of divergences, discords and dissonances,, but trying to remedy that challenge by creating divergent worlds, with borders between them. Completely irreducible differences and discords can be seen as belonging to different worlds, while others can be resolved. This produces 'a florescence of extraordinary accords', which might also be seen as valuing harmony at the expense of melody. This is only a temporary solution, though, and new incompossibilities were to appear in the same world, where harmony was disrupted by a new chromatic scale, 'an emancipation of dissonance', the 'dissipation of tonality' and the emergence of a new 'polytonality'(93). Chapter seven. Perception in the Folds We need a body as a 'moral deduction'. I think this means that we need it because 'primary matter', which appears as something obscure in our minds, needs to be 'extended', and to encounter 'resistance or antitype' (97), and this means an individuated body [that can interact with other individuated bodies]. [We have just assumed the need for a material dimension here, of course -- it all sounds a bit Hegelian]. However, Leibniz also tells us that our mind has a clear and distinct zone of expression, and somehow this also leads to a requirement for a body. In this case, the body expresses a relevant part of the world, so that when Caesar crosses the Rubicon, it enables the river to be put into 'proximity' with his body, his immediate environment [which implies some sort of conscious linking of bodies and environments? Or is it just that the body is a convenient unit for the environment to influence?]. Bodies are able to condense a number of events at an individuated level; these appear as predicates of a monad; they belong to a monad and are incarnated in its body. The clear zone enables this ongoing relation with the body. The body has a role of exploring the clear zone. This seems like a contradiction between a passive and an active role, and between obscurity and confusion, as opposed to clarity and distinction. How can bodies express anything clearly and distinctly, when its movements are 'known only in obscurity' (98). In the terminology of Leibniz, however the singularities of each monad are extended until they contact the singularities of each other. This extension is obscure, and finite, so that knowledge of the entire world is necessarily 'dark'. That knowledge appears to monads only in the form of minute elements, as 'hallucinatory microperceptions' not as a grasp of real objects. There is a state of 'fog… Death or catalepsy... Drowsiness'. The infinite number of tiny folds inside the monad are constantly furling and unfurling in every direction, so monads appear as 'agitated sleepers who twist and turn'. The microperceptions or little folds are representatives of the world and they are intricately folded, sometimes together. However, we rely on these minute perceptions to produce our 'conscious clear and distinct apperceptions'(99), and the former are always present as elements, whether recognized or not. These minute perceptions, and the transitions from one to the other produce the classic state of disquiet, an element in pleasure as well as pain, and they govern the watchfulness of the animal, or conscious awareness of influence post hoc. They are indistinguishable and not clearly perceived, unlike the macro folds that produce apperception and appetite. Again, there are not just psychological dimensions to this argument, but metaphysical ones as well, since this is how the infinite world is expressed in the monad. Conscious perception of the world means 'spiritualizing its dust', it is a matter of totalization, but this is not just a matter of adding together parts: 'the totality can be as imperceptible as the parts' (100—yay!), when it becomes, for example, part of a background. Instead of parts and wholes, we're talking about the relation between the 'ordinary', and 'what is notable or remarkable' [in the sense of coming to our attention?]. We can express this 'literally—that is, mathematically' as a relation between two heterogeneous parts that produce a singularity [the example given is a differential equation version of the formula for a circumference]. Similarly, colours can be perceived as separate, but they are also in a differential relation [connecting two colours -- green is the differential relation between yellow and blue that may not be themselves detectable]. We can even explain hunger as the differential relations between the elements that we require that would eventually produce 'something notable or remarkable' in acute hunger (101), and there is the sound of the sea as differential relations between heterogeneous sounds. Even the position of a sleeper can be seen as the folding together of different relations into an overall good position: '"Good" macroscopic form always depends on microscopic processes'. To come to consciousness, things have to cross a threshold, seen as 'so many minimal units of consciousness', infinitely small perceptions. Some are then selected and linked in differential relations to produce the particular quality perceived by consciousness, such as the colour green. The ones that remain inconspicuous can still be seen as 'requisites or genetic elements, "differentials of consciousness"'. This provides the 'psychic automatism of perception'. It is not that objects simply directly affect us, rather that the object has first to be established as a perception in particular conditions of space and time. This affects real and mathematical objects alike. Even space and time are not just simple givens, but rather 'the nexus of differential relations in the subject', while 'the object itself ceases to be an empirical given in order to become the product of those relations in conscious perception' (102). In this way, eternal objects are actualized in the subject, and figures in spatial coordinates. Nevertheless, this does not imply infinite understanding, since there is always an unconscious, 'a nonself in the finite self'. Nor does this indicate any divine understanding. It is rather the presence of the world in the finite self, 'the infinite present'. Apparently this also is found in the notion of a 'baroque equilibrium or disequilibrium'. We can now return to the issue about clarity and obscurity [which is quite important for Deleuze, and appears in his Logic of Sense, probably in the form of a critique of positivism, although that might just be my over-simple reading]. For Leibniz, clarity comes out of obscurity and is always returning to it. Here it is Descartes who is being critiqued for trying to establish rigorous separations. Differential relations in obscurity are drawn into clarity, into clear perception. Differential relations are crucial in selecting those minute perceptions involved, 'Thus differential calculus is the psychic mechanism of perception, the automatism that at once and inseparably plunges into obscurity and determines clarity'. This automatism works both universally and individually. At the first level, the process works to produce similar conscious perceptions in all existing monads, since the same differential relations are involved [so we all see a colour green at the same spot in the spectrum]. At the second level, 'actualization is different for each monad', [so your precise understanding of green might be different from mine] since each monad prefers some differential relations over others to provide it with 'exclusive perceptions', or it works on some relations, and not others. These perceptions must be compossible, however. The universal level provides the common world that is expressed by all, the individual level produces the specific clear zone, as a subdivision. Clarity emerges from obscurity in this way, but it also plunges back into darkness. It is always a matter of more or less clear. Not all the monads will attain the same level of clarity. Both obscurity and clarity belong to bodies. If clarity is a kind of filter of the elements in darkness, there might be other filters to give what is distinct rather than confused. Differential relations play the role of the filter, but they operate at different levels, and never in an absolute way. In particular, clear perception is never distinct, but only '"distinguished," in the sense of being remarkable or notable' (104). Another filter is required to see that the remarkable is regular, and also to extract singularities, 'the inner singularities of the idea or of the distinct perception'. There might be another filter to select out the ordinary, through the notion of the adequate or complete. Together, these filters 'constitute a circular system', and we can now see that 'like Balthazar, "Everything is ordinary!" and "Everything is unique!"'[We seem to have veered quite a long way towards the role for the subject here though, with the material world only providing the basic elements for the minute perceptions? Maybe the differential relation is also a part of that material world?] To recap, we have met three notions of the singular:
Going back to perception, all monads express the world darkly through an infinite number of minute perceptions, only distinguished by their distinct zones of 'clear, remarkable, or privileged expression'. It is possible that some monads do not possess such a zone at all and are '"totally naked"', living in darkness, in vertigo, with nothing acting to produce clear perceptions, and therefore possessing nothing remarkable. This is how we can see death as a limit for monads: living ones will always have some kind of capacity to recognize bits of the environment, food or enemies, and this gives them 'a "primary force"' (105) which can never be explained by physical or chemical activity alone. Actions outside produce 'inner perceptive activity', and this is the soul. In some animals, like the tick [much used example elsewhere eg TP], these are very simple perceptions—light, scent of the prey, and a tactile awareness of where to burrow [not Leibniz's example but someone else]. Nevertheless, it might be possible to see some scale existing between animals on the basis of their increasing perceptions and widening zones of clear expression. Some monads can 'remember' by linking this zone with others. Still others can extend and intensify zones and connect their conscious perceptions, becoming 'reasonable or reflexive monads', where they do not just attain clear zones, but something which is distinctive or adequate. Only the damned are excluded as before. So we can classify monads in terms of their perceptive qualities. A follower of Leibniz, Fechner, has developed this classification as types of spiritual mechanism. He also suggests that monads can vary in terms of their ability to perceive, sometimes receding back to an animal-like state and then regaining consciousness. Minute perceptions from outside invade consciousness and force selection, especially if our conscious efforts are checked. It is like 'a dust of colored perceptions' (106), but each molecule of dust contains minuscule folds 'that are endlessly unfurling and bending on the edges of juxtaposed areas'. When we regain consciousness, we can fold these molecules, joining them together, controlling their speeds and selecting among them, producing 'the solid fabric of apperception'. This is a secondary fold for a secondary type of perception, and unfolding should be understood as the movement that goes from one to the other, sometimes folding minute perceptions, sometimes unfolding them, deliberately to explore our perceptions. [Typically, Deleuze refers to '22 folds' in a person, but this is referenced to a poet. I suppose we should be glad he actually referenced it this time!]. In this way, it is often the case that we unfold between two folds, hence 'perceiving within the folds'. However, perceptions do not relate directly to objects, nor to 'physical mechanisms of excitation'(107). The only physical mechanism involves differential relations among unconscious perceptions, and these have no object themselves. They do have metaphysical significance, however, in alluding to the world outside the monads, which [of course!] only exists through monads. These metaphysical mechanisms are folded in the monads, and in this way, unconscious perceptions should be understood as representatives of the world, 'and not representations of objects'. This is different from modern psychological conceptions, but it is important for Leibniz's system, indicating a circuit between the microscopic and macroscopic, the metaphysical differential relations and the psychic ones. We always perceive in folds, but this is a matter of constructing figures without objects, even though those figures arise from the haze of dust of minute perceptions. We can see these folds [and there is a nice example of a herd of animals raising clouds of dust through which we can perceive various figures like arches and windows]. So there
are two stages of deduction, first from the
monad to what is perceived, but here we
encounter [the problem of idealism via]
Berkeley, and we cannot conclude that actual
material bodies exist, not even our own.
We only have perceptions. However, Leibniz
argues that what is perceived has a double
structure. Macroperception arises from the
differential relations among microperceptions,
and what this means is that any phenomenon,
anything that is perceived must be collective
'like a herd, an army, or rainbow' (108) [we are
going to quibble about this notion of collective
in the next chapter]. This collection is
given a mental unity by differential relations,
and differential relations themselves are
reciprocally determined by 'relations carried
out necessarily through thought'. The
issue is whether or not there is anything
outside thought and perceptions, some material
force which engenders bodies, external to
monads.
Leibniz argues that there must be bodies, because otherwise, the number of 'perceiving substances' would be limited to human beings or angels, whereas we know that the universe is both varied and stocked with animals. Another argument 'is even more bizarre and complex'—that what is perceived resembles something 'that it forces us to reflect upon' (109). [The example is that there really is a substance that produces the perception of whiteness, or some actual material that produces the sensation of pain]. What makes this complicated is that Leibniz is not saying that perception resembles an object, but rather 'evokes a vibration gathered by a receptive organ', an organ which focuses all the tiny movements in the flesh that produce pain. It is like the process of projection: 'pain or colour are projected onto the vibratory plan of matter'[we are using vibrations here in the same weaselly sense that Deleuze uses them, to develop some notion of cause at a distance?]. This gives us an analogy: just as minute perceptions relate differentially to produce conscious ones, so vibrations of matter relate differentially to produce the organ. In addition, the resemblance to something in what is perceived is not direct representation. Descartes argued that perceptions represented extension, at least if they were clear and distinct, whereas obscure ones could be seen as just signs without representativeness. Leibniz is different, however, and invokes the notion of a projective geometry [the example has a circle projected on to a flat surface to give a parabola] for all perceptions, which thereby turn into '"natural signs"'. What they resemble is 'matter in extension, vibrations, elasticities, "tendencies or efforts" in motion' (110). Pain resembles but does not represent, molecular movements in matter. Resemblance itself means something that resembles, not something that is resembled [again really a definitional way of getting out of the dilemma—perception grasps resemblance as a process, but this process is still like normal resemblance, because it's produced by the matter itself]. When we perceive something, we produce matter in conformity with a relation of resemblance, 'the likeness that is itself the model, that makes matter be that which it resembles' [so reciprocal determination again]. How does this resembled 'come forward' as material? There is no general physical mechanism like the psychical mechanism in the soul. We have excluded external causality. There may even be the claim that we have to deal with necessary fictions, just as Leibniz sometimes argues that the differential calculus is a convenient fiction. We can change the question [!], and ask whether differential calculus can explain infinitesimal [relations between actual] things. The role of differential relations, however is only to extract clearer perceptions from minute ones, a psychic mechanism, relating back to hallucinatory perceptions and psychological realities, but not physical ones. We cannot just assume that physical reality corresponds to psychical reality, although we can suggest that as a convenient fiction. Physical mechanisms are different, however, and feature waves and displacements moving through molecular movements [which can be understood as '"conspiracies" of molecular movements']. When we come to defining bodies, we have to see that there are two essential characters: first bodies can diminish infinitely because they have infinitely tiny parts; second, they are in constant flux, exchanging parts. Physical mechanisms do not involve differentials, but more conventional movements like the ripples caused by a stone being thrown into water. Matter must be 'full of organs' to contract these waves or vibrations, gathering together infinite causes, [and turning full lists of causes into effective causes]. [It seems that] psychic causality, emanating from each monad also focuses this general extrinsic infinite causality, as it perceives the universe, and this is different from the tiny parts constantly being exchanged with it. We need two kinds of calculus, one that relates to the 'psycho-metaphysical mechanism of perception', and another that refers to 'the physico-organic mechanism of excitation or impulsion' (111). These two are still connected [mustn't allow dualism], perception can still resemble physical vibrations contracted by the body, with consciousness 'corresponding' to the conditions of the organ. [Apparently, this conception was at the heart of one or the differences between Leibniz and Newton. The latter tried to calculate movement of a fluid matter and its physical effects, but was not so good at accounting for the relation between different parts—maybe. Leibniz was better at explaining psychic mechanics, and Newton and physical mechanics. The differences were metaphysical as well as mathematical. Although Leibniz only talks about links between ideas and matter in terms of resemblance, 'we must recall that it is the likeness that is the model, and that it determines whatever it resembles'(112)—having it both ways as ever]. All this shows that monads actually require a body, as 'primary matter', and that this means they are also composed of secondary matter [matter as we normally understand it?]. The way the second deduction goes is by arguing first that perception displays 'a relation of resemblance with a material receptor that receives vibrations'; then that we can call these receptors organs or organic bodies which 'constitute the vibrations' that they receive; that physical mechanisms are not identical to the psychic mechanisms, but they do resemble each other; God has created things so that matter resembles him, 'a presently infinite vibratory matter (of infinitely tiny parts) in which receptive organs are distributed everywhere, swarming'[God solves the problem]; in this way, an aspect of perception is that it now helps represent actual objects in conformity with organs. All this can relate back to what folds do. Perception establishes folds in the soul which decorate the monad on the inside. However, these also resemble matter, which we can see as 'organized in outer pleats'. Perception 'straddles the micro folds of tiny perceptions and the great fold of consciousness', while matter itself has 'tiny vibratory folds' which are amplified by organs. Folds in the soul resemble the pleats of matter 'and in that fashion they are directing them'. [So folds are the main forms in which resemblances work] [I wonder what the modern alternative is, without God—contingent connections between perceptions and matter? Modern physicists cease to worry about whether their perceptions resemble matter or not? I also wonder if God is not central to the whole folding metaphor -- something that is everywhere and in every separate thing but not as particles etc]. My clear and distinguished zone of expression arises from 'the primitive singularities, ideal virtual events to which I am destined' (113). I have a body because of this clear zone. I can only express clearly that which concerns my body and will affect it—so Caesar becomes the spiritual monad who best expresses the crossing of the Rubicon. So far, the argument helps us 'recover ordinary language' [that is, we can put in straightforward terms?]. What happens in the soul represents what happens in bodily organs [which themselves represent the world] , so monads. 'can [even] be said to "suffer"'. However, a deeper problem might exist, connected with causality [cliffhanger, setting us up for the next chapter]. Chapter eight The Two Floors [We encounter the problem with all 2-level explanations, linking (virtual) theory with the actions of concrete reality. In material reality, there are different notions of causes, and finite limits -- Deleuze uses the term 'extremum' and I found a nice basic account which illustrates actual movements and possibilities for the resolution of forces or entropy in equilibria, as in the basic possibilities: These
represent stable, unstable,neutral and
metastable equilibria respectively. There is
also reference to a 'caternary' curve -- that
formed when a chain (caternaria) is suspsended
from either end -- could be stable equilibrium
as above but with a different curve.The point
is that this notion leads on to all sorts of
modern stuff about vectors and attractors, and
the terminiology used in DeLanda, like
states of systemts etc.
We are going to 'solve' the problem of linking the two levels or floors using dogmatism or incoherence as ever. There will be God or a magic substance -- vinculum subtantiale -- as well as the usual slippery and ambiguous definitions etc]. We start with Leibniz arguing that totalities are not just collectives, not just names. There is the notion of the collectivity which depends on shared or distributed individual qualities. Monads, for example, are a collective in that they share the same relation to the world. They are 'each, or every one for itself, while [other, external, material] bodies are one, some, or any' (114). Totalities of this kind are distributive, with relations of parts and wholes, as opposed to bodies which are merely aggregates, where one relates to the others [at the same level). The upper floor of the monad, the soul, belongs to the distributive totality. In the material universe of bodies, we find movement, propagating waves and interactions. Whereas monads express the world, bodies are impressed by other bodies. This gives us two different regimes and two different sorts of cause. Souls are in 'vertical immanent causality' with the world, while bodies are in 'transitive horizontal causality'. In the first case, we find notions of liberty or grace, final causes and moral necessity, in the second one, we find efficient causes, physical laws and only hypothetical necessity '(if one is…, so then the other…)'(115). Yet these two must still be seen as connected, as two halves, We have already noticed that there is primal matter or primal force, arising between the minute perceptions of the monad, differentially related. In this way, the object becomes something 'perceived or the world as expression'. However, we need a different understanding of the other parts, the material part, which is not affected by the pure relations, but by those that produce efficient causes, producing bodies which can only resemble perceptions. Here we are talking about 'empirical laws of second Nature'. Here we find empirical singularities, like the extremum. Curves are now finite, with definite coordinates, minimum and maximum, not just 'vectors of concavity' that defined inflection and inclusion. We can now determine the position of objects on such curves as effects of efficient causes [the forces at work, like gravity and other extrinsic vectors]. We can calculate particular curves, or contours, measure actual areas, determine movements, including vibrations affected by specific frequencies, and the interactions of 'all kinds of derivative forces, elastic and plastic alike'(116). So there are two equations of the world, one in minds and conceptions, and one in nature itself. How are they related? For Leibniz they have to be 'concatenated 'or continuous [arising from the monistic and universal nature of God again?], so a calculus applies to both, and so do differential relations, although they do different things—producing 'a maximum of quantity of being' in the first cases, and concrete relations in an equation in the second. The dominant singularity in the material world is the extremum, but the other 3 are also connected, and presuppose it [the other singularities relate to more general properties of curves and have developed the mathematics of curves first?]. In this way, the two floors are related but also different. The upper floor of the baroque house displays weightlessness, the lower floor the 'gravity of mass', and they are connected by vertical transitions 'spiritual elevation and physical gravity'. Others have talked about the differences between structures and figures [the latter being empirical shapes, as it were, while structures refer to relative positions]. A disciple, Ruyer, insists on the connection, however, in 'substantial or individual forms', although we can work with figures as having an autonomy of their own. The vertical dimension explains the soul of the monad, its ability to survey itself [and reflect], its quality as a superject. [Usual anti positivist sentiments, denying the complete sufficiency of the empirical world and accounting for our ability to vary it in thought -- essential to a critical position says Zizek]. We are not just talking about autonomous objects grasped by conventional subjects, but a notion of self presence, an absolute interiority, that displays self fulfilment and self enjoyment [developing perceptions regardless of material influences from organs or extrinsic forces]. Absolute forms can oversee the whole operation of perception, unconstrained by local linkages, and not just functioning to understand the empirical, but forming themselves. These processes affect not just living organisms but even inorganic particles and molecules, although in different varieties. These forms are the primary forces, or primary unities, and they are 'actualize a virtuality or a potential'. They also have a relation of harmony with each other. [Then an aside on gestalt theory 117 – 18, explaining the structure of perceived figures and physical structures. A connection is established with a dispute between Leibniz and Newton, which partly turned on the 'critique of vacuum' and notions of attraction. If I recall accurately the discussion in Kuhn (Structure of Scientific Revolutions) , Newton was at odds with those who held a more mechanistic view of the universe—he actually specifies Descartes—who saw a mysterious ether filling the spaces between objects like planets, with forces traversing the ether literally by vibrating adjacent molecules of it. Newton's originally bizarre idea was that the planets actually attracted each other with a mysterious new force, gravity, that operated even across vacuums, without having to transmit vibrations. How it did actually work was clearly a philosophical problem, but physicists cheerfully ignored the problem, eventually anyway. Maybe, Leibniz is on the side of the mechanists here? Deleuze is arguing that, at the time anyway, his notion of thrusts and impulsions instead of attractions works just as well. He says more contemporary uses of 'the laws of extremum' to explain organic phenomena still work with assumptions about preformed paths and abstract forms generally, and if we abandon those, we end with 'linkages without sufficient reason'. However, do we want to preserve the notion of sufficient reason? The whole use of the term 'vibration' in Deleuze, to explain the ways in which one series can affect another, or one point another for that matter, has always struck me as anachronistic. Is Deleuze still using the preNewtonian understanding? If so, why? Does it explain chaosmos better than Newtonian physics? He wold want to go beyond Newton, no doubt -- but why back to mechanicism? He seems evasive here, so we never know if he is giving his opinions, or paraphrasing those of Leibniz, in the famous indirect free discourse]. [For Leibniz] empirical laws relate to collections, masses and organisms, not individual beings and the primary forces that constitute them. They explain the distribution of 'derivative forces', and the distinction is really what is at stake when distinguishing the organic from the inorganic. It is a matter of distinguishing the individual from a collective phenomenon, an absolute form from [empirical] 'massive, molar figures or structures'. Again, these phenomena live on different floors. However, it is individual beings that operate sufficient reason through their forms and primal forces, and it is these that make up collections as secondary. This is not to say that the lower floor is in some way merely secondary and composite, since 'Clearly [!] , one level is folded over the other' (119). The levels have different sorts of folds, creases or 'bends of matter'. The difference between organic and inorganic can be explained in terms of different folds as well. The bends of matter manage to hide their influence on the boundary between the floors, however, while the folds of form on the upper surface are open to self examination, revealing the details 'of an absolute surface that is copresent with all its modifications'. {Shows the limit of 17th century philosophy that had not developed any empirical analysis of social influences on thought?] We can see this in terms of a virtuality being actualized in the monads. The only way the world can be actualized is in monads, even though this is conveyed through each monad 's point of view. But there is another process at work as well, involving the possible and the real. Once God has chosen the best world, the other worlds are still being actualized in their own monads. In other words, a number of actuals can be possible, without being 'forcibly real'. There is a further stage, where the actual is realised. There is only a possibility of being realized. The issue is still related to the monads and their perceptions, since perceiving, which 'requires a resemblance of the perceived to something' is itself a form of realization [here we go with ambiguous terminology]. Realization arises from something that happens in bodies, that makes bodies themselves real or substantial [another ambiguity is about to be introduced through the notion of substance]. So we have actualization in monads and realization in bodies, but how does the world manage to produce both? What is it that is being actualized and realized? We can perceive and experience events, like a physical blow which my body receives and my soul feels as pain, but what about the other part of the event, the bit that is not realised and actualized? There must be another secret part, 'a neutral singularity, incorporeal as much as impassable', something which originates in all expression and all realizations, the eventum tantum 'a pure virtualityy and possibility...the pure predicate' (120) [According to Kirkeby (2004) the eventum tantum is 'a concept used by both Heidegger and Deleuze... [Meaning]… "The great events" or "so much of the event"… This concept transcends both ontology and epistemology… [It is] the prototype of the event… that which is beyond Sameness, and hence beyond both the concept of identity, and beyond its negation [similar to the term non-aliud] a term in language, which defines any representational structure. It denotes that it can neither be defined by affirmation and nor by negation… [It] could be a way to grasp the concept of an absolute immanence, a mode of existence, which implies no distinction between "outside" and "inside", between thinking and thought, and between subject and object in a process of time. {Pretty magic substance then, and quite handy in the circumstances} The genuine event is the shape, which absorbs knowing into the known… [Leading to the definition] "that it has everything outside itself, except the knowledge of having everything outside itself. The event is totally dependent and totally autonomous, at the same time'(291 - 2). The world can be seen as 'the "pure" reserve of events that are actualized and realized'. Leibniz requires this preexisting world, this element of the event [since those bits of the events which are expressed and implemented are not the totality— nor do they just add up to the totality], and that there is 'a potential that exceeds the souls that direct it and the bodies that execute it'(121). It is the material universe that is expressive, [Reality 2 as opposed to the normal Reality 1] both to the world and to the soul. Actualization and realization are different regimes of expression: 'one is distributive where the other is collective'. Actualization by monads is internal and independent of others, while realization at the level of bodies involves relations with other bodies, ultimately, the totality of bodies, the whole material universe. The first process goes from whole to part, from the entire world to a zone of it; the second one relates parts and parts, near to far, from the expression of its related monad, to the zones of expression of others. However, luckily, there is an accord between these regimes, or harmony, between the soul and its body, and therefore between other souls and other bodies in its surroundings. However, we still have a problem because the soul is an 'each or every,' while the body is a 'one'. What forms the connection between one body and each monad [and here, Deleuze is is going to use the phrase 'appurtenance', which implies possessions]? Leibniz here is engaging in an old debate about the union of the soul and the body, about incarnation. However, harmony might explain the correspondence between each soul and the universe [because this has already been defined as a relation between parts and wholes], but there are still problems explaining the correspondence between the soul and the body. The relation cannot just be an aspect of the body [I'm not sure why, you can define it however the hell you like --maybe this would introduce a hierarchy?]. Instead we need 'a theory of appurtenance', or belonging (122). Husserl gives us an example of a theory of appurtenance, in the fifth of the Cartesian Meditations [discussing how we know about others] and this refers to Leibniz. For H, the monad is replaced by the ego, the self has a sphere of its possessions, and in that sphere of appurtenance, I can find something that I do not possess, something foreign to me, something objective, an other. Leibniz has a similar strategy, and asks what belongs to me, with the answer that it is all the thoughts of the self, the cogito, and because thoughts are so diverse and changing, the predicates include the entire world as perceived -- or rather the entire world that I express clearly. This is still my world, and I own the primary matter in it, especially my body which I can use and coordinate what is perceived. This body is uniquely extrinsic, however, foreign and objective as above. The difference is that Husserl was to go on to argue that we can apperceive the other as another monad [through the assumption of reciprocal perceptions and so on], but Leibniz had already assumed that there are other monads, and seeing everything outside my clear zone as indicating their existence, as 'a community of monads' [sic]. Together, they express all their clear zones to make up 'a first Nature': there is no need for bodies. Monads do not contain others, but those others can be assumed because we can see their mark in the obscure zones within me. For Leibniz, actully meeting others means encountering a second Nature [something that really does contain unexpected elements?]. Leibniz further [bullshits] by saying that body and soul are both distinct and inseparable. It is a particular kind of harmony and union that produces real distinctions together with inseparability [I am reminded of Durkheim and the hope that organic solidarity would provide a social bond between separate and autonomous individuals]. There is some notion of a general connection with other bodies, because the monad knows them only through resemblance—so its own body must be organic, resembling the body of another man or another animal. Leibniz drags in God to further argue that the body must be organic, that is provided with organs. [Delirium awaits]: the body is made up of an infinite number of material parts collected together, but also able to form organs, as a result of 'crowds of little monads, monads of heart, liver, knee' (123), according to their special zone. These monads belong to parts of my body, and are requisites of it. It then seems to follow that since these little monads are capable of perception, so must my body be [could be wrong here—certainly matter itself is seen as inseparable 'from these little souls capable of perception']. Overall, Leibniz's theory of appurtenance produces an endless inversion [infinite regression] — monads that have a body are different from monads that are specific requisites of this body, or parts of it, and they in turn possess a body, other than a collection of requisites for another body, and their body 'possesses crowds of tertiary monads' -- and so on. In this way, soul and body are different, but they're always undergoing 'the coming and going between one level and the other', and this defines their inseparability [physical inseparability as opposed to logical inseparability—slippery concepts again]. My body is a collection of smaller monads which are always in flux. Those that once belonged and now depart are only '"pro tempore" prerequisites', nonsymmetrical or temporary ones. The latter produce 'the revelation of a half-other'(124), 'the animal in me as a concrete being'[good Leibnizian grounds for becoming-animal, then]. By contrast, Husserl never sees the human body as decomposable like this, and the animal part of ourselves is only an anomaly [a weird echo of this in volume five of Proust, which I have been reading, where our hero sees illness as reflecting some independent animal-like qualities of the body]. For Leibniz, we have already assumed that there are other human bodies, but it is the animal that now 'springs forth amid my effects'[the organs are seen as animal like], and it follows that our body contains '"an infinity of creatures that are also worthy of life"'[with a reference to a Leibniz letter]. Actual animals are only an enlargement of the smaller ones, producing an animal psychology and an animal monadology, and Leibniz needs this argument. It is difficult for us to know what does belong to us and what does not, and phenomenology is no help here [the example is Beckett's Malone, who apparently has trouble listing his possessions]. However, the notion of possessions becomes important for philosophy, which can now put 'the element of Having in place of that of Being' (125). A list of what things possess helps us classify and develops the notion of Being [apparently, Tarde was on to this, 125]. Leibniz had already been talking about the diverse thoughts of the monad rather than just the act of thinking, and we have already seen how perceptions of predicates, as properties [geddit?] have replaced the notion of attributes. Working out how bodies act involved all sorts of relations among the possessions, including 'inversion, turnaround, precariousness, and temporalization'. This in turn emphasizes continually changing relations among the monads, despite their [spiritual] harmony and union. The final implication is that monads have as their properties not abstract attributes such as 'movements or plasticity', but relations to other monads, some of which they possess [subjugate, dominate, or appropriate], so these are also power relations, and include the power to fold or to contain something. Again, the baroque generally featured 'the crisis of property' (126), with the emergence of new machines or new living beings in the organism. Appurtenance requires domination, to make little monads cohere to produce my body, and to be able to renew it with new little monads. In spelling out what this domination means, Leibniz envelops the term substantial vinculum, 'a strange linkage, a bracket, a yoke, a knot, a complex relation that comprises variable terms and one constant term' (126). The constant term is the dominant monad, and this vincular relation belongs to it. This produces problems, however. Other monads are its variable terms, the ones that are dominated, but the dominant monad cannot actually own or contain the others, as predicates of its subject [because no monad can contain the other monads by definition]. Here, we have a relation not of subject and predicate, but one that is substantial. However, every relation must have a subject, so the dominant monad must still be the subject of the substantial vinculum [otherwise, the substantial vinculum must have no subject, and therefore just appear in some free floating way]. We have to get round this by arguing that in this case, the dominant monad is an unusual subject, 'a "subject of adhesion", not of inherent or of inhesion'. This looks like a real problem for Leibniz, 'an almost insufferable paradox', because so far, the notion of a preestablished harmony between the monads has implied no outer relation, 'but only ties regulated on the inside'. The substantial vinculum looks like an extrinsic possession, 'the relation that clearly has the subject, but that is not in its subject, and that is not a predicate' (127). How can the monad, as an absolute interiority, suddenly possess another side, the one that seems important, 'strictly complementary'? [My notes on Look's article reveals the extent of the apparent contradiction or paradox. Deleuze proposes to resolve it, through magic]. We can think of it in topological terms. The monad is unilateral, closed off by a particular 'torsion of the world, an infinite fold, that can be unwrapped in conformity with the condition [of closure of the monad] only by recovering the other side, not as exterior to the monad, but as the exterior or outside of its own interiority; a partition, a supple and adherent of membrane coextensive with everything inside'[so a magic fold solves the problem, with a magic outside that is also an inside]. This makes the vinculum 'the unlocalisable primary link that borders the absolute interior. [A diagram on page 127 doesn't help, but I reproduce it].  The dominated monads appear in the relation as objects, but they can exist without the relation and vice versa, because the relation belongs to the constant monad and not to them. The relation can actually acquire an infinity of dominated monads. If they escape submission to this vinculum, they are grounded by another one attached to another dominant monad, although they can also be completely free [below] . The vinculum works by first acquiring its variables [the dominated monads] as a mass, although each monad keeps its own individuality, and must do. Then the vinculum 'extracts a "common modification"' (128) [the metaphor is that they form an echo when they are reflected on the surface of a wall. The vinculum itself is the reflecting wall, as a kind of outside of the dominant or constant monad]. In this way, the vinculum produces a mass effect from individual variable monads, producing a collective echo, an amplification of individual whispers [and, particularly mysteriously, 'the passage from optics to acoustics']. This mass acquisition produces an inversion of the normal relations of appurtenance when we consider the relation of the monad to its body. Normally, the body belongs to the monad, but when they are acquired as a mass by a vinculum, they are the ones belonging 'a infinity's material parts that are inseparable from them' [the parts that make up the dominant body?]. The parts are both homogenous, so they can be replaced, and heterogeneous because they play different roles for the dominant body and have to be coordinated. As a membrane, the vinculum acts as a grid filtering available monads in order to make up organic parts. As parts, the bodies of the variable monads are not the same as the [original, primary, defined] body of a constant monad. This composite organic body possesses the dominant, as 'a body that here finds the determination of its specific unity' [some general body? An actual or real organic body, as opposed to a simpler, predefined one?]. Something else emerges. The vinculum is attached first of all to an individual dominant monad, and helps determine the individual unity of the body that belongs to it—my own specific body. We can presuppose this as a function of the vinculum [by pursuing classic tautological philosophical reasoning]: 'there would be no specific unity if individual unity were not already presupposed'. The organic body must persist as a unified one despite the coming and going of the bits which make up its parts. So we have 'a cycle of the body and the soul', beginning with 'Every and One'[the soul and the body as above, and then returning to 'Every' [probably a different kind of every, though, not the definitional one that we started with, but something more like any individual every?]. To sum up, each individual monad possesses a body inseparable from it; each one [also] possesses an [organic] body because it is the subject of its vinculum; the vinculum assembles a mass of variable monads; these masses become infinity's of material parts, which make up the organic composition of an [organic] body, under the control of the vinculum; this organic body is the one that belongs to the individual monad, produced as an individual unity by the vinculum. [I still think this is not just a circular relation, because the body means different things at each stage—that's why I have insisted that the second kind of body is qualified by my adding the term organic. This could be wrong? It certainly looks more profound and mysterious if you don't do this!] We have to remember that we can classify monads, according to their clear zones of expression: reasonable monads have a wide and intense zone which means they can reflect and deepen their insights, so they can 'tend towards God' (129). However animal monads also have their own clear zone, even ticks, or monads of the liver etc.. We can therefore consider each monad to be 'a simple substance, a primary active force, and inner unity of action or of change'. The monad has a body and is inseparable from it [which explains its ability to act in the clear zone], but the monad does not contain the body, and is 'distinguished from it' [monads are always souls AND bodies]. However, a monad needs a body because its power to act is limited considered as primary matter [here rendered as 'initial matter ("moles")']. All reasonable monads are dominant, but to a lesser degree, so are all monads, all have requirements, and dominance even survives death [described here and elsewhere as a kind of dispersion of little monads]. Monads are 'immediately present in the body, but only through projection'[this seems a bit of a leap, and I'll have to go back and check the argument]: this projection enables the projection of active primary force at a point in the body. Reasonable monads are never dominated, animal monads are always dominated, although they also dominate in their turn. Domination by reasonable ones takes the form of being acquired as a mass, in clusters, not in terms of the bodies they possess, but in terms of the material parts of which they are aggregated, so the body of dominated monads get incorporated into the bodies of dominant ones. The vinculum attached to an individual dominant monad does this, acting as 'a knot'[I still don't see the significance of this metaphor—something interwoven?]. We can reserve particular terms for particular stages of this process, using aggregates to refer to material elements, clusters to monads. Aggregates of material parts are the things that make organisms—they are active but also collective and derivative, '("plastic forces")' (130), and in their mass state, they can generate and corrupt organic materials, 'through envelopment, development, and fluxion of material parts'. They are no longer projected, but collectively related to material parts, 'they are themselves said to be material' [as 'second matter'], corporal or composite substances [by magic, they have been realized in material forms!]. However, this requires a dominant body itself to have a living organic body. This applies to all secondary matter. Primary matter requires a body, a secondary matter, an organism emerging from a crowd of monads. Yet we have seen that monads organize inorganic aggregates. There must be some derivative forces on secondary matter, structures and figures in the material aggregates themselves, produced by forces that tend towards equilibrium, the extrema. We are not just talking about any external forces, but special ones that produce these phenomena. They are 'effectively those of dominated monads' (131), and are connected deeply with their individuality [as usefulness for a dominant monad], as projected on to the dominant monad ['exist only in the pure individuality of the dominant as a primary force of surveillance']. The derivative forces occupy a special place between mere statistical collections and individual distributions. We can use them to understand the behaviour of crowds. They describe not purely collective behaviour but something 'more interindividual and interactive'. This is what makes them organic [secondary matter here is also called 'clothed matter']. They affect aggregates, 'but belong to the organisms'. They produce figures, structures and also textures in matter. This was understood in baroque conceptions as texture being underst/l ood and produced by 'a generalized organicism, or… a ubiquitous presence of organisms'[and the example is Caravaggio's paintings!]. Secondary matter is clothed, meaning that 'matter is a buoyant surface, a structure endowed with an organic fabric, or that it is the very fabric or clothing, the texture enveloping the abstract structure'. The notion of interindividual and interactive clustering implies temporary appurtenances, 'provisional possessions', as parts come and go from aggregates. This hints at an explanation for the transformation of species, although Leibniz referred to mutations, or associations and dissociations, 'metamorphosis' (132). This involves a capacity to envelop and develop parts, and a 'fluxion' that affects parts as they enter and leave different aggregates. There can be 'free unlinked monads without a vinculum', however. They are aggregated like the particles of felt, pressed together. They comprise inorganic bodies or elements of bodies, [not proper bodies, not like those that belong to monads], 'substantial components, semisubstances'. The bodies are purely mechanical, following mechanical linkages. They are actualized phenomena, but must have monads after all, or they would not follow natural laws: the forces they exert are not plastic ones [what a lot of convoluted and backwards pointing argument! All necessary only to preserve consistency]. So organic and inorganic bodies obey laws because their 'inner nature' enables them to do so—hence the universal application of something like the law of gravitation. The preestablished harmony between monads works in every case, not just occasionally [and apparently there were 'occasionalists' at the time]. We can also not rely on miracles or any divine mechanisms to explain general laws. There therefore must [!] be in inorganic bodies 'a third species of monad'(133). These are neither dominant nor dominated, with some weaker kind of the inner unity. Dominant monads 'are unities of the inner change', dominated ones 'units of organic generation and corruption'. The third species, 'degenerated or defective monads' are 'units of outer movement', concerned with determination, or mechanical linkage—all only possible because of the 'inner unity' of these monads. In this sense, Leibniz agrees with Bergson [and other philosophers briefly mentioned above], that extrinsic determination requires some 'inner unity of the trajectory', with the determination as a means, or sometimes an obstacle. The inner trajectory is produced by 'an active elastic force', pervading the universe, energized by aggregates, or 'defective monads without a vinculum', and appearing as tendencies. Leibniz argues that force and action are the same thing, operating in different ways according to the types of monads. Dominant monads actualize, as a kind of power in action. Dominated ones are not passively collected under a vinculum without developing their own kind of power as 'dispositions or habitus' [a sort of background power to influence?]. The third kind develop tendencies [they seem to be dynamic on their own, so the extrinsic force that animates them does so by removing impediments to action]: these tendencies only last a split second, but they are future -oriented and their energy passes along to the next instant to produce an 'inner unity of movement' (134), so they are 'flashing, twinkling in a way', illuminating matter. We have to clarify derivative forces and how they are linked to different types of monad. Derivative forces seem to be 'material, accidental, modal, "states of a substance" that are exerted on bodies'. But we should not understand term 'state' as referring to a predicate contained in a subject. Instead, the term refers to 'status or a (public) aspect'. Derivative forces are primary forces except in terms of their status, which arises from their being organized by a vinculum, taken as multitudes and turned into either plastic or elastic forces. Derivative forces are therefore the result of several substances in a crowd or mass. They still belong to a body 'are present to a body', constituting their '"material souls"'. They are requisites for a body constituted by a multitude which is itself a primary force, produced by projection [the combined force of lots of the smaller monads?]. It is possible to think of the composite producing derivative forces as a public status [and apparently, this is how Whitehead used the term]. Leibniz uses 'public' to mean the derivative state of the monad, and private as referring to what they are in and of themselves, 'their primitive condition'. As public, they belong to a composite body which is not their own, even though they constitute it. Reasonable monads are private in another sense, because they have no public status as defined above, and nothing that can be derived from them. [They seem to be like private individuals in civil society, subjects of God]. The three classes of monads also refers to their entelechies [roughly, self defining organisms, or the vital force that actualizes organisms]. Some only have perceptions, animal souls have 'memory, feeling and attention', reasonable ones have minds. It might be that being reasonable explains their domination, and animals are placed in the relation of both domination and dominance according to their capacity for reason. It is also a matter of the state of the entelechies, however—some can be 'tied to a body, in a heap' (135), a kind of degeneration, and this explains variations within the overall categories. Souls and matter or bodies are distinct, and 'each operates according to its own laws, one by inner spontaneity or action, the other by outer determination or action', but there is no direct interaction between the two. However, we can specify 'an "ideal action"' (136), where something bodily is the cause of what happens in the soul, as in suffering, or than something in the soul causes something to happen in a body '(a movement taken as voluntary)'. In the normal state of affairs, the world is expressed as two distinct expressions, actualization and realization, but we can use the notion of an ideal action to suggest that there are occasions when the two might be combined as 'an "ideal cause"', 'the best expressant'. There is only one world, and it is both actualized by souls, and realised by bodies: we can think of this with the metaphor of heavenly and earthly cities, or the two floors of the house. We can further subdivide the house into private apartments on top, and public or common ones below, [primary and derivatives respectively] , the individual, and the collectives or totalities. Unlike Kant, for Leibniz the two floors are inseparable although distinct, with 'the presence of the upper in the lower. The upper floor is folded over the lower floor'. It is not a matter of the one acting on the other, but rather one belonging to the other [so folds supplant {and incorporate} causes]. The soul becomes the principle of life 'through its presence and not through its action', and, in general, all 'force is presence and not action'[I thought we had agreed the two were identical, or at least always found together]. Bodies project into souls and vice versa [this sort of projection is well discussed, in the beginning, I have just remembered], bodies are requisites of souls. Possessions replace the notion of action, and souls do not act upon bodies even when they possess them. This belonging involves 'a strangely intermediate, or rather, original zone', which helps bodies acquire individuality even as a possessive, if they belong to a private soul, or, when souls become public, to a crowd or some other collective body. This produces a material fabric linking the two levels, with the upper folded over the lower, so that 'we can no longer tell where one ends and the other begins, or where the sensible [material] ends and the intelligible [cognitive] begins' (137). Where is the fold moving [found]? It moves between essences and existences, between the body and the soul, between the inorganic and the organic for bodies, and between the species of monads for souls. It is a 'sinuous fold, a zigzag, a primal tie that cannot be located'. There are also different looser types of linkage, not just vincula: they only binds souls to souls, producing the 'double [two way] belonging' which connects them [again, I thought the substantial vinculum also linked to material parts of bodies—there must be different sorts of vincula, no doubt]. The looser connection arises because the soul possesses a body which might be possessed in common by other souls as well, hence the 'perpetual overlappings of the two floors'. This sort of connection enables us to posit ideal causes, working both ways [between actualization and realization]. This sort of connection also permits us to insist that souls can also be material, and forces mechanical [depending on what sort of connection between the two we are talking about, and at what stage in the sequence?]. We have a variety of syntheses, in matter itself, produced by 'laws of exteriority', and in souls, under the action of the vinculum, or through the tendencies which flash, as above. Bodies are animated by souls because they belong to them: in practice, only souls have an inner action, with specific laws, which bodies realize, according to their own laws. Actualization and realization are folded together, both in souls and in bodies, and affected by the two regimes of laws. This double fold is a zweifelt, as above, producing a crease or seam [but not a split]. Bodies are not themselves real, but become real only after something has been actualized in the soul: it is then completed by being realized in the body. The soul has to perceive something first, so realization in the body is 'the realization of phenomena' (138). The fold itself is a product of realization [so, in the strange backwards terminology of philosophy, 'what is realized is the fold of the two levels']. So is the vinculum as another fold ['the fold of the two levels… [is]... the vinculum itself or its replacement']. What we have in Leibniz is a 'transcendental philosophy of the event', which features 'the double operation of transcendental actualization and realization (animism and materialism)'[I have often thought that Deleuze's universe is an animist one]. Chapter nine. The new harmony. We can think of folds in simple terms as in textiles. When we clothe human bodies, the fabric is not just subordinated to the body, especially in baroque costume, as in the rhingrave-canon [below].  The effect of baroque clothing is to overwhelm the wearer, freedom from conventional space [with lots of examples of painting and sculpture to follow, 139-140]. The style alludes to something 'placed between clothing and the body'(140), 'the Elements'[the classic four elements]. We see in painting, and above all in sculpture the effects of these elements, of the breeze that makes the ribbon below, or flattens the cloak, the far older us, the effects of water as in Goujon's bas reliefs [below].  Clothing is autonomous, and not just decorative, expressing 'intensity of a spiritual force exerted on the body', to alter it, but also 'to turn it inside out and to mould its inner surfaces'. In this way, the Elements can be seen as derivative forces 'that materialize an infinite spiritual force' The fold appears in 'everyday recipes or modes of fashion as well' (141), in still life, with its drapery, 'jewelry that burns with folds of fire', vegetables 'caught in their earthy folds'. These paintings are packed with folds, which could never be unravelled except by going to infinity, where we will encounter the spiritual. Since 'the law of extremum of matter entails the maximum of matter for a minimum of extension', we get an overflowing, sometimes even when matter flows out of the frame as in trompe l'oeuil. Sometimes this is an unfolding upward, into airiness, but more often it is in terms of length and extension, width, the depiction of extensive masses. There is also extension by prolonging one art into the next, from painting extending into sculpture, then into architecture, and then eventually into city planning: one art form provides the 'frame' which can be detached and extended into the next. Overall, the arts combine to form 'a universal theatre', that includes the elements as well, and where the city becomes 'a decor' (142). The whole of public space, the Socius, becomes 'the sum of the arts'. This anticipated current collapsing of boundaries between the arts, again with its forms of 'folding and unfolding, wrapping and unwrapping'. Frames open out on to unlimited space, heading only towards a new form of unity, both 'comprehensive and spiritual, punctual… conceptual'. This is the notion of the world as a pyramid or cone, with a material basis, and the luminous apex as origin or point of view [the latter provides a form of individuality that is easily 'reconciled' with 'full continuity', just as in the discussion of the point of view earlier]. The cupola is the 'baroque figure par excellence', sometimes with an apex that has a concave surface instead of a point, extending the notion of infinite folding. Sculptures of the human body also incorporate this notion of massive base and upper unity, derivative forces and primal force respectively. Unity cannot exist without broad extension, and the universe is seen as centred, still something produced by a summit or point of view [the current view is to see the world as a theatre or a dream or illusion, says Deleuze]. A spiritual presence is somehow realizing itself and unifying space with 'hallucination'. We also need to understand the baroque as offering allegory. Benjamin argued that allegory is not the same as a symbol, which 'combines the eternal and the momentary', because it 'uncovers nature and history according to the order of time' (143). Both symbol and allegory link concepts to objects, sometimes not single objects but rather an idea that develops the concept, and sometimes not single objects, but a series of them. Allegories appear in 'devices and emblems' [the example is the porcupine standing for "from near and afar", because it was thought to erect its spines when year, but also showed them from afar]. These devices have 'images or figurations, inscriptions or maxims, and personal signatures or proper names of owners', permitting 'seeing, reading, dedicating (or signing)' (144). Considered as basic images, these devices break out of their frames as allegories to 'form a continuous fresco' or cycle, not just refer to an essence or an attribute. They refer to events which have histories or series, antecedents and sequels. Inscriptions are also propositions which point to 'an inner concept', not just the subject and an attribute ['from near and afar' is itself a predicate], and they also relate to an individual subject, appearing as the owner, who possesses individual virtues or qualities. Together, we get to the particular baroque notion of the concept, 'a "concetto" or an apex', a kind of unity of different propositions and images of cycles and series folded in the individual subject, or the universe imposed in the baroque world. The notion of a cone is important, and sometimes even this is depicted as an allegory. Leibniz provides the philosophy for this conception, transforming perceptible objects into figures or aspects, subject to a law of continuity, and working out the relation between events and these figures, inscribed in propositions. He then goes on to relate these propositions to an individual subject, defined as an apex or point of view, and collects those individuals in terms of the principle of indiscernibles 'assuring the interiority of the concept and the individual'. A new relation of the one and the multiple emerges: 'the one must have a multiplicity "of" one and the unity "of" the multiple'(145). Others have suggested that ones must also be related to ones, and multiples to multiples more directly [I think the implication is to retain the different notions of the multiple as distributive where it relates to the one, and collective where it relates to aggregates] Again we see the importance of appertaining or belonging to. This is also the key to allegory, so 'Leibniz's philosophy must be conceived as the allegory of the world… but no longer is the symbol of the cosmos'. The notion of the pyramid of possible worlds explored in the Theodicy [above], and this combines 'figures, inscriptions or propositions, individual subject or points of view with their propositional concepts [properties?]' (146). We get a new dynamic: 'description replaces the object, the concept becomes narrative, and the subject becomes points of view or subjective expression'. We have already seen the link between horizontal extension and spiritual vertical unity, and there is no suggestion that one precedes the other. The process can be illustrated with baroque music, already recognized as an ambiguous combination of intellectual order and 'affective pleasure', from vibrations impacting on the senses. Melody operates horizontally, but harmony works vertically to establish unity. Harmony can be extracted from melody, constantly restoring higher unity to the dispersion of melodic lines, and this offers a general definition of baroque music. There is some doubt whether Leibniz meant musical harmony just as a synonym, or whether he actually meant it more literally [to describe the reality]. Certainly, preestablished harmony does have an important role in resisting occasionalism [above]. Harmony relates multiplicities to a definite unity with distinctive traits, later to be defined in terms of 'Existence, Number, and Beauty'(147). Harmonic unity is also a numerical unity, and this makes it possible to derive individual existents. Individual notes imply an existing harmony, so '("to exist means nothing other than to be harmonic")'. We perceive harmony only aesthetically, 'in confusion', but we can thinking out in terms of simple numbers [apparently, specifically, irrational numbers]. Leibniz was also to understand unity in terms of the inverse or reciprocal numbers—the 'denominator shares a relation with the numerical unity [1] as a numerator' (147), and the harmonic appears in other mathematical terms such as harmonic mean, harmonic division, and, eventually, 'the harmonics of a periodic movement' (148). We can see these examples as demonstrating the link between harmony and monads: 'monads are initially harmonic', initially, because they are designed like that by God, to express the world, to become an existent in harmony with the whole. We can also see the monad as a numerical unit, a number, a simple number, and, in Leibniz, 'the inverse, reciprocal, harmonic number'. We have already seen how the monad is the inverted image of God, one over infinity, not infinity over one. This is what is meant by preestablished harmony, and it also serves as 'an original proof of the existence of God', if we can infer this existence from the way in which the monad works [as we did, in a rather dodgy way, earlier]. The inverse number is infinite or infinitely small, a part of the natural number in the distributive sense. Inverse numbers are not identical with each other, implying that harmony is a reconciliation of individuals, not seen as parts of some universal spirit. This is 'pantheism'(149). [an account of the work of a more modern mathematician eventually refers back to the infinitesimal series as a further example—this series never entirely adds up to one, but does express a region or zone of one, 149]. The work of the monads is to establish differential relations and integrations upon the part of the series appearing in their clear zones. This can be seen as a matter of presenting 'accords' between the state and its infinitesimals, 'establishing differential relations among infinitely small units that are integrated into this state'. We can consider affective 'accords' as well, involving the calculus again, but this time in explaining things like the noise of the sea [as above, the synthesis of lots of little noises], or the [musical only?] chord. In this sense, the monads produce chords as well as accords [Jesus!]. At the human level, accords are produced from the constant state of disquiet mentioned above, integrating infinitely small perceptions to make one clear one. I am particularly able to do this if I am operating with my own own clear zone, while I cannot do this with everything else. However, monads are linked together to produce another type of accord. Leibniz might have borrowed this conception from the musical model, at least through analogy, but developed to a new level of rigour. Thus the monad can produce its own 'major and perfect accords', especially if this follows reflection. This is a particularly pleasurable form of harmony, detectable even in the middle of suffering, as when martyrs experience joy[and cf counteractualization in Stoic conceptions of death in Logic of Sense] . However, these accords can link with other accords, and combine with them in various ways, as 'mirror accords', for example, simple inversions. There can also be 'dissonant accords', where dissonance is resolved in acceptable ways, and this is like reconciling elements of pain which always accompany pleasure, displacing it to an acceptable level, suppressing 'resonance or resentment, by avoiding passivity, by pursuing the effort to suppress causes' (151). This is regarded as a 'good' way to manage dissonance, whereas the damned produced diabolical ways, through resentment or hate of god, getting pleasure from pain [somehow, they still 'make possible the infinite progression of perfect accords in the other souls' however — a note refers us to a French reference]. The whole process is 'spontaneity', the production and transformation of accords ending in a resolution or modulation, aspects of the expression undertaken by the monad. The monad can be seen as existing 'so as to extract accords from one part of the line of infinite inflection that makes up the world'. This is 'self enjoyment'. [Deleuze notes that this might be a contradiction with the earlier description of constructing differential relations, but says that Leibniz does not care!] We return to the notion of harmony as vertical while the line of the world is horizontal, and remind ourselves that this has always been the case. This leads to a second kind of harmony, however, 'concertation'. [as when different instruments of an orchestra combine in a concert?]. Monads are linked to each other, and this can generate accord between their own spontaneous accords. It is another example of the effects of the fold passing through [linking] different entities—the floors, Nature and God, the material and the soul, and even different sorts of substance. All these effects are produced by the initial harmony between the souls. We also find harmony between the little monads and the dominant ones as above. However, spontaneous accords exist only on the inside of every monad. Luckily, they can join together in a choir, says Leibniz, singing in perfect accord without even being aware of the other. This follows from the links we have already explored, from overlapping clear zones. There is even 'a law of the inverse' at work, so that for every monad that conveys obscurely, another monad conveys clearly. We can also see this as a matter of cause and effect, with clear expression as the cause, and obscure expression as the affect [almost a notion of musical resonance here?]. This will only be one of those strange ideal causes though, 'without real action' (153). This suggests something more established than the law of the inverse: that is too simple because clear zones can expand and contract, and sometimes even overlap, so it is a matter of more or less clarity. There are also processes that augment or diminish clarity. Back to causes at the level of bodies. Some statements of cause are ideal, while some take the form of clear propositions [the example is a bit odd—the ideal cause here is some initial statement that a movement of a boat causes the water to be displaced, while the clearer proposition specifies in more detail, for example that it is the prow that pushes the water aside]. So relations of cause can involve a movement from clear to obscure, as above, but also movements from the more to the less clear [also describable as the confused or the less stable]. There is this notion of diminution here in sufficient reason as well, where clear expression 'increases in the cause, but… diminishes in the effect'[and some connection with the ability to perceive immediate causes because they are more clear and stable, while we can only get the resemblance of the broader causes, say of pain]. Any road up, 'concertation is the sum of ideal relations of causality'(154), moving from the more clear to the less clear, and this is perfectly compatible with spontaneity, since spontaneity helps to clarify something in the monad. So we get to linked aspects of harmony, spontaneous accords, on the one hand, following inner reason, and correspondence between them on the other, deployed through normal space and time. A further implication is that every major and perfect accord is [must be?] accompanied by a minor or dissonant record in another monad. Combinations are possible without identical accords. Monads can even relate to what the other one is producing, responding to concertation [while also remaining spontaneous, of course]. It follows that space and time are not empty but are vectored, by this 'order of coexistence' between the monads, and this explains why harmony is preestablished. In fact it is twice established, once by inner reason and spontaneous expression, then again through concert. Deleuze says that this suggests that communication in the world is constant and preestablished, still useful [for him] as a modern equivalent of sufficient reason. Usually, vertical harmony is subordinated to horizontal melody, and here we can talk more about a specific vinculum rather than a preestablished harmony. We see this, for example in the way in which a continuous bass structures a tonality for the chords. However, any vinculum also gathers clusters of dominated monads producing material aggregates, and this provides 'a new freedom and unity, or a flux' for the melody, escaping the structure. There are other points of contact, for example counter point ['bi-univocal correspondences among points on diverse lines' (155)]. Melody can also introduce all sorts of other variations and foreign elements including delays and interweavings , even a unique motif across different tonalities. We can generalize from here to talk about the ways in which 'melodies of development' operate in the material universe producing 'Nature [as a] immense melody and flow of bodies', and none of it contradicts the other spiritual inner unity. Indeed, the former depends on the latter which provides it with a body just as with monads: the way in which melody appears to join together my senses helps me 'recognize harmony in the real'. Harmony and melody are themselves in harmony, and this is how the soul links to the body, the intelligible to the sensible, and the sensible to other elements of the sensible in extension. Everything fits together because of folds which fold these things together [fold=harmony now, or is harmony and additional force linking things?] . This seems to be an exact analogy between philosophical and musical harmony in the baroque. Leibniz was even able to predict inexplicable melodies, an example of what we have already seen as 'excessive representation', produced by some direct connection to feeling. Other definitions of baroque music include vertical harmonies, in chords as well as other intervals, dissonant chords, concert involving contrast inner voices and instruments, melody encounter point, and continuous bass to consolidate tonality [what better example could you get than some of the famous organ works by JS Bach—follow the link here for one of my favourites. Too obvious and vulgar for Deleuze I expect ]. Leibniz continues with a musical analogy by examining different relations of body and soul, 'influx, chance and ...harmony', which can be compared to two different ages of music. However, we must not think of binaries between text and music, but rather folds. Again, the baroque stressed the need for accords to structure affect, including the way that voices develop particular inflections, and to explain the pleasure of listening to the music and following the text. Here, the relation is one of '"fold - in" or… "fold according to fold"' (158). Since the baroque, accords are no longer so important, but the baroque, and Leibniz, have evolved, and can be seen in terms of different points of view, different figures and grounds, with the new notion for the monad, not the closed chapel, but 'the sealed car speeding down the dark highway' [attributed to an unreferenced Tony Smith]. Things have changed because we no longer think in terms of possible but divergent worlds which have already been selected, and which already assures some consonance between the monads. Now there seems to be no underlying selection. Nor does harmony retain its privileged, permitting unresolved dissonances, divergences, no tonality at all. This makes the monad straddle several worlds [with a strange analogy about being half open like a pair of pliers, 157], unable to contain the entire world. As a result, it is no longer centred, but follows a spiral trajectory away from the centre. Vertical and horizontal harmonics are no longer distinguished, and this implies that spontaneous of vertical private harmony is no longer separated from public concerted melody. Instead, 'the two begin to fuse on a sort of diagonal' (157-8), monads penetrate and modify each other, and there are mobile groups of prehension that carry them along and offer only 'transitory captures'. Stockhausen or Dubuffet [see below --he wanted to mix high and low aesthetics, apparently] have collapsed the boundaries between inside and outside, public and private, and replaced 'monadology with a "nomadology"'(158). However, 'we are all still Leibnizian, although accords no longer convey our world or our text. We are discovering new ways of folding, akin to new envelopments, but we all remain Leibnizian because what always matters is folding, unfolding, refolding'.  Thank the Lord!! Back to Deleuze page |