| Brief notes
on: Deleuze, G. (2007?) On Leibniz Dave Harris NB online so no page numbers for quotes It is useful to look at a life of Leibniz, by Prenant, so that we can get an idea of writing styles in use at the time, even though Leibniz exaggerated them and we also find his work develops not only in books, but in letters and memoirs. We can see Leibniz as a great example of what a philosopher does, how a philosopher creates concepts, just as artists and musicians create. It follows that concepts have to be created. Science also creates thought, but not concepts exactly: art is closer; both are a matter of working with flowers, dividing organizing and connecting them 'around certain singularities'. Philosophers do not even have to be intellectuals, as long as they can extract singularities from flows of thought, from inner monologues. Even nonphilosophers have to use concepts invented by named philosophers, who sign them. Some of these signed concepts seem appropriate to us in particular circumstances, and we need not become a complete disciple. Concepts are ways of living as much as thoughts, hence what counts is the 'creative activity .. not… a reflexive dimension'. But at the same time, concepts can appear as far away, as arising from 'the scream'. Philosophers don't sing but scream—they need concepts, and we need to trace the concept back to the scream. It is not just a matter of having passions. Leibniz is a rationalist, a philosopher of order, including organizing the city. However, at the same time, 'he yields to the most insane concept creation that we have ever witnessed in philosophy'. It all stems initially from the notion of universal reason. Some approach the problem calmly and rationally, as does Descartes, working on the basis of an entire tradition, and still coming up with a new concept as in the slogan 'I think therefore I am'. Leibniz creates a whole batteries of new concepts, partly as a result of the power of the German language: he is mathematician, physicist, jurist, and politician. He is not always admirable, for example, when he conspicuously failed to defend Spinoza—'Leibniz is abominable'. He also had a sense of humour. He built a philosophical system with several levels which 'symbolise each other'. These levels are used as he argues with people at different levels of insight themselves, which makes the texts look incoherent and contradictory: we always need to evaluate the level at which he is working. He is a 'very difficult philosopher' with strange or as he calls them 'funny' thoughts, almost like science fiction. He was very interested in games, and suggested establishing an academy for games, which would straddle a range of disciplines as a source of 'universal exposition'. His work can be summarized as consisting of a number of principle propositions. The first one is the principle of identity, which can be rendered as saying that a subject produces an attribute or predicate which is logically reciprocal—a triangle is a triangle. In some cases, this helps us uncover even more attributes, as when we say a triangle has three angles [true by definition] and it also follows that a triangle has three sides. This is a logical necessity, but not the result of reciprocity: it is inclusion or inherence. So we have two kinds of propositions, reciprocal and those demonstrating inherence or inclusion. Other way of putting this argument is to say that 'every analytical proposition is true'[must be, because it is either tautologous/reciprocal, or logical/inherent, inclusive]. In analytical propositions, the predicate is identical with the subject or included in the subject, and to get to predicates, or we have to do is interrogate or analyze the subject. So far so normal, and we haven't really got on to proper philosophy yet. The new thought arises from thinking out reciprocity, and this had to be thought through, because it met a need. We consider the inverse of the statement of identity above and argue that 'every analytical proposition is true'. This is not tautologous or obviously logical, or need not be. What it means is that every true propositions must be analytical whether we want this to be the case or not, [we are implying that we will be able to analyze true propositions because a true statement must contain within it, necessarily, certain predicates which will emerge, whether or not we welcome them]. There must be attribution and predication already contained in the true statement. If we think in terms of concepts, the predicate of the concept is either reciprocal with its subject, or inherent in it.[I think we have a slight of hand here -- two notions of truth,one empirical and one logical, as logical positivists might say. The 'true' in the first case every true statement is analytical -- is a logical truth. The 'true' in the second case is really an empirical statement -- 'every analytical proposition is true' is really a claim that analytic propositions point to some truth about reality, that reality is organized like that so as to produce analytical statements, which means it must have predicates {or events} contained in subjects and all that. Then there is a confusing weasel since we are denying that it is real subjects only notions of subjects, which makes it a logical truth again -- but then we let real subjects slide in. I don't think any of these C17th 2-level explanations work, not Leibniz nor Spinoza -- Delanda has rescued Deleuze by saying you need some modern physics to explain changes in state]. We have to work this out, however, because not all judgments about reality seem to be matters of attribution or inherence. Consider statements such as there is a box of matches on the table: we have a spatial determination, but no predication or attribution. There are also relational judgments, where X is larger than Y—we can be reciprocal here and say that Y is therefore smaller than X, but again we don't exactly have predicates. So is the judgement of attribution universal, or just one form of judgment? There are three kinds of judgment cited here already —relational, spatial, and attribution, and then again maybe many more like 'judgement of existence' like trying to work out the qualities of god, but adding 'if he exists'—his existence is not just an attribute. Leibniz must therefore show how all propositions 'can be linked to the judgement of attribution' nevertheless, and things like relations, localizations and existents should all be seen as the equivalence of attributes. This is going to be 'an infinite task', and if pursued, it is going to produce a strange world. We also have to redefine our terms a bit, because it's the case that not every analytical proposition is true [for example the famous attributes of fictional people or animals like 'the present King of France'?]. On the other hand, Leibniz insists that 'every true propositions is necessarily analytical'. This leads us to the principal of sufficient reason. Everything must have a reason. The principle means that 'whatever happens to a subject... everything that is said [truthfully] of a subject must be contained in the notion of the subject'. What is the notion? It is something also produced by reason—reason is precisely the notion itself insofar as it contains all that happens to the corresponding subject' [classic circularity here, it seems to me, where sufficient reason requires a 'notion' of the subject, and, happily, the notion is itself a product of reason?]. The notion is a characteristic signed Leibnizian concept So reason involves a notion of a subject, which must contain 'everything said with truth about this subject'. This notion clearly underpins the reciprocal identity principle which sparked off the whole philosophical investigation. It is going to produce a 'bizarre world' where 'everything that you say with truth about a subject must be contained in the notion of the subject'. It is also going to be a lot of work to demonstrate this. As Leibniz thinks about the implications, he is going to develop some 'truly hallucinatory concepts' in his metaphysics. It arises from connection with the original scream [likened to delirium here]. We can understand this 'conceptual madness', however. First, though, it looks like Kant offered the notion of synthetic judgment to accompany analytic judgments, and this can be seen as opposing Leibniz—but this is not disagreement, merely a new concept: philosophers no more contradict each other than painters do when they develop different styles. To take Leibniz's actual examples, it is true that Caesar crossed the Rubicon ('we have strong reasons to assume it's true'), and we can also makes statements such as 'Adam sinned'. These are propositions about events ('event-ual'). The argument is that the predicate, 'crossed the Rubicon' must be contained in the notion of the subject Caesar, if it is to be true. This notion contains everything that happens, as long as we can make truthful statements. This is the 'concept of inherence. Everything that is said with truth about something is inherent in the notion of this something'. This leads to something endless, however. Unlike Aristotle, Leibniz does not know where to stop, even when a chasm opens. The problem is that the notion of the subject contains everything that has happened to that subject, and this would involve ultimately 'the totality of the world'. We can see this by considering causality: the things that caused Caesar to cross the Rubicon can be extended to infinity, as all causes can be, because they themselves have causes. It also follows from this that sufficient reason is something more than cause: causes can only ever be necessary but not sufficient. Sufficient reason however 'is the notion of the thing… Expresses the relation of the thing with its own notion, whereas cause expresses the relations of the thing with something else'. Effects similarly stretch off themselves to infinity. As cause links with cause, the whole of the world becomes 'encompassed in the notion of a particular subject'. This gives to philosophy 'a trans-historical characteristic'. It also invokes another term—not inherence or inclusion, but 'expression', so 'the notion of the subject expresses the totality of the world'. That means that each of us do as well. This raises the possibility of 'the single subject, a universal subject', with individuals just as appearances of the subject. Leibniz had to repudiate this view, however, because this would simply take over [reduce] the argument about notions and sufficient reasons [classic philosophical argument!] . In this he offers 'the first great reconciliation of the concept and the individual'. This came as new, because concepts were thought as something general, applying to several things: concepts referred to generalities, individuals to singularities, and individuals could not be reduced to concepts: individual characteristics, such as possessing a proper name, cannot be generalized to produce concepts [there is no concept of Dave-ness, although we might be able to make empirical generalizations about them]. Leibniz always worked with the subject as an individual, the singularity, and we can generalize this into 'the perpetual formula in his works: substance (no difference between substance and subject for him) is individual'[apparently, Leibniz weaseled subsequently to say that even the notion of God did not prevent substance being irreducibly individual]. There is an implication for individual freedom, since it follows that Caesar [as a notion anyway - and here we have pretty well slipped in a statement about the empirical Caesar? Are notions separate from actual empirical subjects or not?] can only unroll, explicate, or unfold 'something that was encompassed for all times in the notion of Caesar'. The action of crossing the Rubicon is eternal [reminds me of Ahab's speech about how the conflict with the whale was eternal and predestined]. Leibniz was forced to address the issue of freedom, while reconciling it with a Christian regime [discussed below]. If everyone expresses the totality of the world, how can we distinguish one subject/substance from another? What is different is the point of view. Again this leads to a series of philosophical concepts, although they take the form, as so often, at first of 'banal formulae', at which the philosopher 'winks'. The theory actually develops following his work in projective geometry, and as part of the general experiments about perspective [in the Baroque]. The point of view is not just produced by the subject, but rather the other way about. Nietzsche was able to pick this up later, and also argue that his 'philosophy is a perspectivism'. It is not just that everything is relative to the subject, this is banal and meaningless. Instead, 'the subject is constituted by the point of view', not the other way about. Henry James renews the argument in his own perspectivism, and makes the subjects in his novels vary according to particular points of view. Indeed, points of view become the 'sufficient reason of subjects', explaining them. It follows that there are as many universes as there are substances, or, in Christian terms, as many completely different representations of god. The points of view defines individual essence, otherwise they would be coterminous with living individuals. Points or view were explored before, for example in portraiture, [and in experiments with anamorphosis—apparently, a portrait of Mussolini also depicted his son in law and the King, depending on points of view]. Leibniz explored it through mathematics and projective geometry [via perpendiculars to tangents converging in concave curves etc --see the book on Leibniz ] . Here, the point of view is expressed by subjects, but only 'in an obscure and confused way', principally because individuals only operate with 'the form of minute perception… Infinitely tiny perceptions… Unconscious perceptions'. Deleuze says there is a clear parallel here with Leibniz and the development of the notion of infinity in differential calculus, and promises to explain more fully later. Here, we can see these minute perceptions as the differentials of consciousness. It means we have our own tiny forms of consciousness, without being conscious of them! Leibniz uses the term apperception to refer to conscious perception. So the point of view that I express consciously is but a tiny portion of the world. It is like having something in focus in your own little zone, while everything around it remains fuzzy, confused, in uproar. The zones can vary in size. They are never the same [and they are not just a matter of subjective knowledge or understanding, but objectively determined?]. In an example [which Deleuze likes], Leibniz says that we can be conscious of the sound of a wave of the sea, we apperceive it as something distinct, but this depends in turn on tiny unconscious perceptions of the sounds of each drop of water as a background. We clearly identify 'one partial result from this infinity of drops' and it is this that makes up our own little world'. In this way, an apperception, a conscious synthesis of unconscious perceptions helps us make our own little worlds in the form of 'clear and distinct expression(s)'. Individual and worlds may not communicate, they may partially communicate through analogies, or they may overlap [as in a Venn diagram]. What guides the particular expressions that we develop is our relation to our body (to be explained below), so that I can never express what Caesar expressed. This has got implications for the conception of the city as well [a term for society?] . It is hard to accept that nothing exists outside points of view, that the world is 'uniquely the common expressed of all individual substances'. Leibniz looks like an idealist here. Since points of view do not always overlap entirely, the world exists only as 'the complication of the concept of expression'. There are problems because the principle of identity also enables us to argue that some things must be contradictory or impossible, where A is not A. This is a relief, because we can at least demonstrate that some events or concepts are logically contradictory, such as a square circle. However, the notion of individuated little worlds is not necessarily contradictory. Leibniz also needs to save the notion of individual freedom as well, to allow the possibility, for example, that Caesar could not have crossed the Rubicon: this would not exactly be a logical contradiction so it needs to be explained. So there is a difference between truth produced by the principle of identity with its logical impossibility of contradictions, and truths produced by the principle of sufficient reason, where contradictory outcomes are at least possible: 'Adam the non-sinner is possible'. Here Leibniz has to distinguish between 'truths of essence and those called truths of existence' [nearly a distinction between logical and empirical truth then?]. Where do empirical possibilities come from, if everything is bound up in the subject? The answer lies in the concept of incompossibility—what actually takes place at the level of existence has to be compossible with the rest of the world unfolds—'Adam the non-sinner belongs to another world… [And]… This world was not chosen. It is incompossible with the existing world. It is only compossible with the other possible worlds that have not passed into existence'. Why did this world pass into existence? We get back to a theory of games. God conceives an infinity of possible worlds, but designs them so that they are not compossible. He then chooses 'the best of possible worlds', [the bit that's parodied by Voltaire's Dr. Pangloss] and this happens to involve Adam as a sinner. Compossibility limits the sphere of logical possibility. For something to exist it must be logically possible but also compossible in the real world. There is a connection with the monad, where 'individual notions have neither doors or windows'. This implies there is no exterior, that 'the world that individual notions expresses is interior, ...included in individual notions'. Nevertheless, individual notions share a common world, since each one expresses not only its own little world, but one that must be 'compossible with what the others express'. This does not arise as a result of communication between subjects, but refers to 'pre- established harmony'. This programmed harmony implies 'the idea of the spiritual automaton', and automata were becoming popular in the 17th century. As a background to the general principles there is a corresponding general problem, relating back to what it is to do philosophy. We know it is creating concepts, and Leibniz is a good example of the 'exuberant creation of unusual concepts'. These concepts can be seen as signatures. We can now explore further 'the notions of Substance, World, and Continuity'. The first thing to remember is the different senses of the term inclusion. Predicates must be included in the notion of the subject if propositions are true, so if Adam sinned, the sin is included in the notion of Adam. This is Leibniz's 'philosophy of predication'. One problem is, as we saw, but this leads to the idea that if a single action is included, so must be all the things that caused it and all the affects that follow, so that we end with the totality of the world included in the notion of the subject in this way, rationalism ends with a kind of delirium, or madness. It ends in perspectivism, remembering that this is not the usual subjectivist kind. So are all relations and all events just predicates? If we look at essences first, we can see that they can be contained in analytical statements, as in mathematical truths, where the sum of two integers is obviously contained in the two integers themselves, indeed, is identical to them. In a particular piece, Leibniz is able to show that every number which is divisible by 12 is thereby divisible by six, or 'every duodecimal number is sextuple'. The way he did this was to show that the number 12 can be seen as something divided by two, multiplied by two, then multiplied by three, whereas numbers divided by six can also be seen as divided by two multiplied by three. So the operation 'divide by two and multiply by three' is included in the operation 'divide by 12'. In this way, a finite series of determinate operations can produce aggregates, as a mathematical version of showing that predicates emerge from the properties of the subject, and inclusion. This is also a way of producing essences, as it were: we already have an essential statement, where any number divisible by 12 is divisible by 12 (the 'pure identity'), but we now also know that any number divisible by 12 is divisible by six. We have used finite and determinate operations to produce this result, that one essence is included in the other. This is how analysis proceeds in maths in general, using 'a limited number of determinate operations'. What about nonessential [non grammatical] truths? The truth of particular events like crossing the Rubicon is not an essence in this way, but a dated event related to existence, as opposed to the eternal truths of mathematics. Nevertheless, that predicate was in the notion of the subject eternally—in all eternity, Caesar will cross the Rubicon at a particular date. 'This is a truth of existence'. [Because his options have already been limited by the notion of compossibility]. Nevertheless, there are still differences between truths of essence and truths of existence, even though, for both, predicates are contained in subjects. The difference lies in that analysis can only be infinite in truths of existence, because we can never finish analyzing the totality of the world that is implied, as we saw. Limited empirical human beings cannot do this, because it lies beyond our experience, so 'infinite analysis… [While technically possible, is]… Created in the understanding of God'. However, Leibniz has also helped to pin down the notion of infinity at both ends of the scale, in mathematics. Although he denied a direct link between philosophy and mathematics, Deleuze detects 'echoes' of the calculus in the philosophical notion of infinite analysis. It suggests a way to solve the problem of what infinite analysis looks like, while using determinate analysis. However, there is also another difference between truths of essence and truths of existence. The truth of essence cannot be contradicted, because the terms have an identity. However, truths of existence can be contradicted—there is a 'contradictory of sinner'. This makes truths of existence 'contingent truths'. However, compossibility produces only one option. Adam not sinning belongs to another world, but so does Caesar not crossing the Rubicon—are these two other possible worlds related? Leibniz addresses this issue by talking about the dream where Apollodorus visits a goddess's palace which contains a number of other palaces—an infinite series of boxes within boxes, all the way down in a 'labyrinth of continuity'. At each of a number of infinite levels, different possible worlds exist, with the same characters doing different things, sometimes with overlaps. The palace is a pyramid. God has simply chosen a world close to the highest level. All the worlds are struggling to come into existence (as an aspect or function of their essences), all are possible in God's understanding, all have a certain 'weight of reality', but the only one that emerges is the best one. This is not the best in moral terms, but in terms of a theory of games, a result of Leibniz's interest in probability. As an aside, it is this originality that has impressed subsequent thinkers such as Nietzsche, who was drawn to Spinoza because there was a 'the familiarity between his very own screams and the concept of the philosopher'. Apparently, DH Lawrence had the same reaction to Spinoza or, and Kleist with Kant. For Leibniz, it was Borges, and the notion of the forking paths as the world of compossibilities all displayed in terms of options and choices. Compossibility is not just a matter of simple contradiction, because the different possibilities are not logical contradictions, but belong to the truths of existence. There is a connection with the notion of infinite analysis. Leibniz explains this in different ways, to suit different readers, as above. In one text he says that predicates are contained in subjects, but either as acts or as virtuality—so Caesar crossing the Rubicon could be a virtual inclusion [only a potential, even if it is actualized]. In another, however, the infinite analysis of the total world would proceed through indefinite analysis, moving from one term to another, all the way down to the infinitely small [as in the series of infinitesimals—see notes on Bos]. In this way, infinite analysis is also 'virtual analysis [in the sense of] an analysis that goes towards the indefinite'—but this is an argument for those with little philosophical background, where virtual is not used particularly rigorously: in more scholarly texts, it refers only to truths of essence [the nonphilosophical version seems to imply that we get to the virtual by simply adding up examples of the actual?]. Overall, this means we cannot use the term virtual to describe inclusion in truths of existence, but only in truths of essence, as in the example of dividing by 12. So infinite analysis [of truths of existence] is not a matter of approaching the virtual, nor is it just indefinite analysis, because this implies that infinity expresses just a limit to what can be done with the resources available, including knowledge; and nor can we just plug in God to get to the infinite. We need something more rigorous. Reverting to the example of the progression of infinitesimals [as a series of decreasing fractions that add up to 1, which is clearer], the bit that continues, the 'etc.' does not preexist but is produced by a procedure [apparently, Kant later could define the indefinite in terms of a synthesis producing an aggregate]. In the 17th century, philosophers tended to have 'an innocent way of thinking'about the infinite, sometimes seen as a mixture of philosophy and theology, but, for Deleuze, that is a post hoc 'stupid' judgment. Leibniz's position eventually became one of saying that the indefinite is virtual in the sense that the terms that point to it are constituted by definite procedures. This is unlike infinity which is 'actual' [must be another sense of actual here, the actual {!} phrase is 'there is no infinite except in act'. It might mean that the infinite is defined only in terms of truths of existence?]. Even for God, there is no end in analyzing the predicates contained in the individual notion. All the terms are given [empirically?], so this is not a matter of indefiniteness, where terms have to be produced by [mathematical] operations. The infinite analysis means an infinity of infinitely small given elements, and this can be seen to be 'actual'[tangible, empirical?]. However we can never in practice reach the end, even God cannot, because it is an infinite aggregate. God gets closer than any humans, though so you can see how things are connected together, like sinning and Adam, joined by 'an infinity of other elements actually given', the entire existing world. So we might pass from Adam the sinner, to Eve the temptress, to the evil serpent and so on. We need to clarify what an infinitely small element is as well, at least for those who are more knowledgeable: it's really 'an infinitely small relation between two elements': relations replace the element. Here, we need to understand differential calculus [and the way in which specific relations become abstract functional ones -- see notes]. What this means is that the inclusion of the predicate in the subject, when talking about existence, is not a matter of identity, not even a virtual one. Identity governs truths of essence. The real relation of interest is the connection between one predicate and another, the maximum possible continuity. Continuity becomes the key to understanding truths of existence, established by infinitely small relations between elements. Continuity defines the world, and discontinuity defines incompossibility. God chooses the maximum continuity as the best. It might be a theological puzzle to establish why the sinning Adam is in the best world, but he is there because he ensures an important continuity, that would lead to Christ and redemption. What we have is a small relation between two different elements, however, but these tend to disappear: they are 'evanescent [vanishing, fleeting] differences', and this is as close as we can get to logical identity. It is the infinitesimal analysis that led to the differential calculus, Leibniz's particular route compared to Newton [see notes] . To understand its significance, we need to discuss differential equations, which are so important in current physics, although modern calculus operates without worrying about the infinite. For Leibniz, the issue was to examine the relation between different powers with different magnitudes and quantities, especially those relating to equations like 'a xsquared + y'. What makes this equation difficult to resolve is that the quantities are noncommensurable [cannot be considered to have the same base units for measure]. The problem is deepened with the discussion of incomparable quantities. The calculus permits you to 'compare quantities raised to different powers'. We can see that it is possible to move ahead with 'a xsquared +y' by first extracting dx and dy. Here it is to be defined as a matter of extracting 'the infinitely small quantity assumed to be added or subtracted from x or from y' [so that we can calculate the slope of the line by looking at the difference between the first and second values on the dimension concerned. When we are projecting this operation into infinity, the differences become infinitely small?]. The infinitely small can actually equal zero, so it is clear that the difference can be the smallest possible conceivable, something smaller than that which is normally measured. Nevertheless, even when the additions or subtractions from x or y is 0, the relation between dx and dy [dx/dy] is not equal to zero. This helps you compare two formerly incomparable quantities affected by different powers, because it moves us away from quantities towards relations, [ratios] and this inaugurates a shift in mathematics towards relations or functions. Leibniz was to argue that the differential was already implicit in ordinary algebra. So when the relation is given values c and e, and both are zero, we do not end with 'absolute nothings', but those that 'conserve the relational difference', so that even when both are zero, c does not become equal to e. This is a 'great mathematical discovery'. The differential relation can be determined. [I think this only follows because we have already decided that there is the relation or analogy between the original x and y, and that this is preserved with subsequent x and y, or in this case c and e. If this relation holds, then if we argue that c and e are equal, when they are set at zero, it would follow that the original x and y must be as well, and this would be 'totally absurd'. Again, it seems like a bit of clever philosophical sleight of hand. Really, the difference must remain because we have already defined it as a constant analogy or ratio?]. We can make similar analogies to argue that 'rest is an infinitely small movements, or that the circle is the limit an infinite series of polygons, the sides of which increased to infinity', or that, as in the diagram of the inverted triangles, the single triangle [ Aec] is 'the extreme case of the two similar triangles opposed to the vertex'. [See the diagram below, reproduced in the book. Imagine the line ec being moved progressively to the right until it runs through point A. Also remember that we are not measuring line lengths exactly here, but more changes in length from E to A etc. The differential compares changes toget a general formula for slopes -- rise over run.] 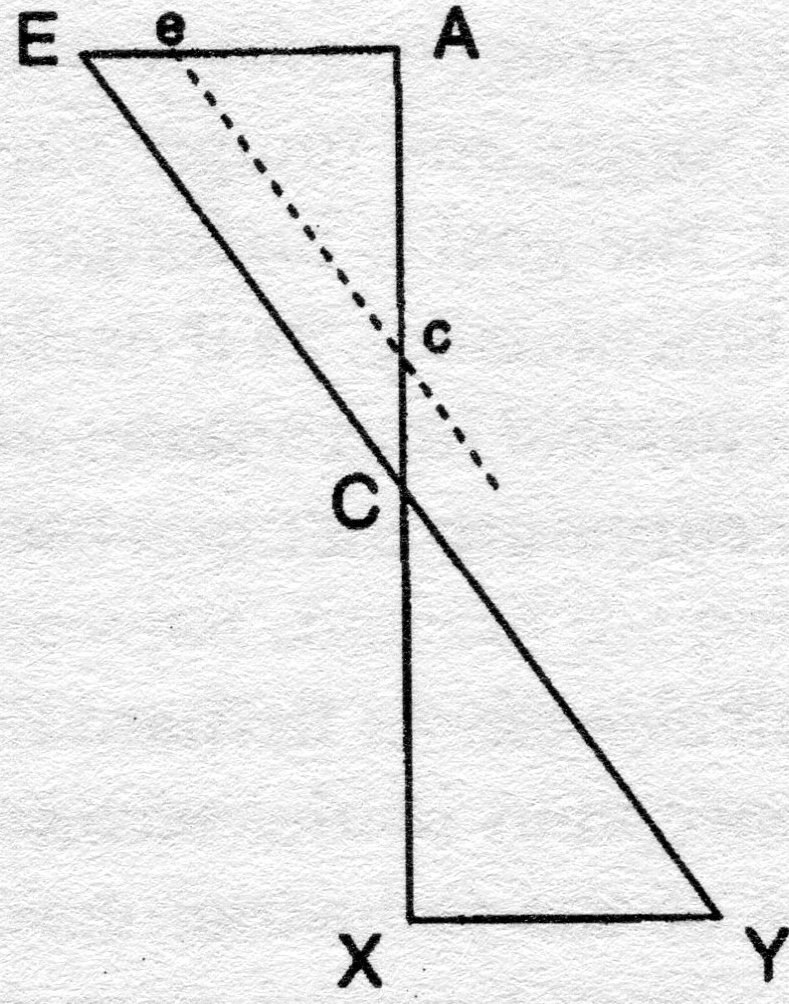 We could say that this particular triangle, located at the point [right at A] where the values of e and c are zero, 'is only there virtually'. The existence of e and c does not depend on their numerical quantities, but because they are in a relation: strictly speaking, the triangle when e and c are at A ec has not disappeared, but it has become 'unassignable '[isn't this just a way of saying that the infinitely small is found at A, not nothing, even though the arithmetical value recorded by zero might be? I think it all depends on Leibniz on infinitessimals: 0 is surrounded by infinitessimals so it is never a static point of nothingness, there are always relations with infinitessimals before and after it, so 0 is always in a relation or a movement. Movement never just stops in an infinite curve. You can say that the circle is an unassignable polygon in the same way— because the sides are infinite [and thus uncountable? Unable to be assigned a numerical value or quantity?]. This is how rest can be considered as a special case of movement, an infinitely small movement. Thus Leibniz can redefine the virtual as 'the unassignable yet also determined'. This is new and rigorous, and Leibniz can demonstrate it relatively easily using the examples above [and getting us to agree that the way he expresses the analogy is consistent— must be one of these semi-implicit propositions that Deleuze's book on Leibniz calls 'enthymemes'?]. What this does is no less than approximate what God does with infinite analysis, [it approximates the divine continuity]. It only describes the maximum of continuity, the extreme case [which is the closest we get to the end of an infinite analysis?], which is plainly included in the normal empirical case [or is it vice versa?] . This gives us the formula of predication. We have to use terms like intrinsic case, to refer to the 'movement the encompasses all movements', while the extrinsic case is the [result of] that movement, the circle in relation to the polygons. We need a concept that 'corresponds to the general intrinsic case and which still includes the extrinsic case'. This will explain continuity between the elements, from the polygon to the circle, [the inclusion of the normal in the extreme as above]. Eventually this was to lead to Poncelot and modern projective geometry based on 'a simple axiom of continuity': take the arc of a circle cut at two points by a right angle. Make the right angle recede and there will be a moment where it leaves the circle no longer touching it. [Somehow] this raises new possibilities for the tangent as an extreme case of this movement: when the points leave the circle they are still there but both are virtual [hard to follow, but I think it is the same sort of argument about the relation persisting even when the concrete values no longer do]. So we have moved from trying to show how the truths of existence are not the same things as truths of essence or mathematical truths. We have shown this but only by having to introduce a notion of infinity. When we are exploring that, we have to resort to mathematical truths again: 'It's funny, no?'. Leibniz has to argue back that he has never said that differential calculus designates reality. It is a convention, a symbolic system which shows how you can designate reality. It's a convention based in mathematics, but it is a '"well founded fiction"'. Calculus uses concepts that are not based in arithmetic or algebra: quantities that equal zero but are not nothing are clearly nonsensical as arithmetic. It is a useful fiction though which 'can cause us to think of existence'. It is a combination of mathematics and Leibniz's idea of the existent, the 'symbolic of the existent'. It is not an arithmetical calculus. We can now see what 'evanescent difference' means—'it's when the relation continues when the terms of the relation have disappeared'. This relation exists in God's understanding, so 'God was only doing calculus'. God is a player, but Leibniz describes the game. He actually has two explanations:
[Deleuze also answers some questions arising] For example that it was not an issue for 17th century people to worry about whether the calculus was artificial or real. Leibniz was clear that it was a 'pure artifice... a symbolic system'. Everyone saw that it was not possible to reduce it to conventional mathematical realities as in arithmetic or geometry. Leibniz never thought that differential calculus offered a complete answer to the issue of infinity, and distinguished, for example between the infinitely small and the infinitely large, which would require different calculuses. There are also qualitative infinities. Leibniz's attempt to argue for different orders of the calculus was only stopped by the 'Kantian revolution'. We find this in history, that problems are defined in such a way is to produce sufficient techniques—geometry and algebra were adequate to classic Greek problems relating to straight lines and rectilinear surfaces. Problems of curves had to wait for solutions: the Greeks modelled curves in terms of 'equations of variable degrees' [eg by drawing innumerable tangents?]. Solutions get exhausted, and this prepares the ground for new ones—but solutions are always connected to specific problems, such as those dealing with terms raised to different powers, itself related to the problem of understanding natural phenomena, which were curvilinear and determined by different forces and velocities. Leibniz introduced the notion of mass times velocity squared, whereas before, physical problems had been confined to calculating mass times velocity, and important issue for modern physics. [After another intervention]. Differential calculus raises the issue of rigorous analysis based on axioms, but this only appeared later. Leibniz was prepared to operate with entirely artificial or metaphysical notions, impure ones that could not be rendered as axioms, and which were therefore, strictly speaking, not scientific. So scientific status was finally achieved, but at the price of sacrificing any metaphysical notions, including those of infinity or limit [with what looks like the use of entirely symbolic not arithmetic terms. Apparently somebody called Weierstrass develops this, as a rather 'static and ordinal' system]. Infinity has changed its meaning, and is now 'completely expelled—we can extract dy/dx just from x and y', [see notes on Bos] although the point about the relation persisting even when the values are zero remains. It still helps us determine further quantities, whereas the axiomatic version does not [except tautologically?]. For Leibniz, we can understand infinite analysis to the extent that the infinitesimal and its continuities 'are substituted for identity'. This further implies the infinite analysis is not grasped by an understanding of identity, but by 'continuity and vanishing differences'. We have to discuss compossibility, however. Leibniz invents this term to be 'entirely linked to the idea of infinite analysis'. Incompossibility can be defined in three ways:
The notion of singularity in mathematics was not particularly developed by Leibniz. Deleuze's analysis here raises the old questions for him about philosophy—does it lead particular terminology, or is it really open to any one without special knowledge? If the first, you have to work with philosophical terms [such as concept, category and so on just like you do with mathematics]. The singular has been classically located in relation to the universal, or the particular as opposed to the general. Nevertheless, a judgment of singularity is neither something particular nor general. Mathematicians extended conventional logic and used the expression as something distinct from regular, something outside the rule. They also refer to remarkable and ordinary singularities, but Leibniz just used the singular as something remarkable or notable, although he gave the second term a special meaning. The mathematical extension helped us replace the old obsession with what was true and false, because 'in thought, it's not the true and false that count, it's the singular and the ordinary'. Kierkegaard was to add 'the interesting'. We still have to find reasons to make the singular as something interesting, out of the ordinary. Mathematics sees the singular as a matter of 'certain points plotted on a curve', or, more generally, 'concerning a figure'. We have to remember that a figure is 'something determined', and that it will include singular and regular ordinary points. So we have a determination for the singular, and a broader definition of determination to include the singular and the ordinary. For example, we can define the vertices of a square as singular points, and these are extensions of the size of the square, points [of inflection] where one line ends and another begins. The lines are composed of 'an infinity of [ordinary] points' What about curves? Are the singular points found at the extremes? What about points where curves meet? Leibniz plots such a graph, on classic Cartesian ordinates, and considers the segments of the curve [and then a puzzling bit, where a particular segment is seen as unique—I can't reconstruct this diagram, nor find an example on the web, to follow the argument, but the conclusion is that a segment can also be unique, or a singularity, and found not necessarily at the extremes—it can be a minimum or a maximum, however, or both depending on which are good. I CAN see this working if we are talking about the point where 2 arcs cross -- this point is unique. Of course, a line segment can be a point, you clot Dave! The other points on the arcs get closer as they approach this singularity.] This is why Leibniz was important, in calculating singularities and maxima and minima, and this is still important today in symmetry or in some optical phenomena. We can now develop the notion of a singularity: ordinary points are below maximum and above minima and also exist in a double fashion [they match on two curves, eg they have the same value on the X axis?]. We can even see ordinary points as another case, 'a singularity of another case' [all ordinary points have the potential to become singular points in different circumstances? I am beginning to see a glimmer of light about how this is going to end in compossibility]. In another example [irritatingly, the transcript is incomplete] a complex curve has singularities that can be seen as 'neighbouring points'. In topology, neighborhoods are where 'something changes: the curve grows, or it decreases'. These points of growth or decrease are also singularities as opposed to the series between two singularities which features ordinary points, going from one neighbourhood to another [clear echoes here of what happens with multiplicities generating a series of singular and ordinary points up to the neighbourhood of the next multiplicity, as in Difference and Repetition -- it wasn't sci fi, it was Leibniz!]. Mathematical exploration of singularity has helped us break the implicit tie that conventional philosophy had to rectilinear figures! Those would not have helped generate the new conception of singularity—we needed to consider complex curves in their own right. [He has obviously had to answer a tricky question, although this is missing. He says he's been tripped up and will need to think about it]. Poincaré also develops the notion of singularity, when discussing differential equations. He identified singular points at crests where two curves defined by an equation pass through each other. Then there are knots where an infinity of curves defined by the equation can intersect. The third type is foci, around which curves spiral in. And the fourth type is a centre producing closed circles of curves. This is another example of where mathematics has pushed philosophical notions of singularity. Something similar can be found in Leibniz. The domain of singularities requires techniques like differential calculus: we can see a singularity as 'the point in the neighbourhood of which the differential relation dy/dx changes its sign', as when curves rise and descend. At the precise point where they change direction, the differential relation 'becomes equal… to zero or to infinity', indicating minimum and maximum again. We see that singularities extend into ordinary points, that 'the theory of singularities is inseparable from a theory… of extension'. This is a definition of continuity, stemming, ironically enough, from the notion of singularity as discontinuity. [Then we leap to philosophical psychology]. It is the same as the connection between ordinary perceptions and apperception ['perception endowed with consciousness']. Unconscious perceptions are necessary, however because they are make up the elements of the global or the relative totality, as a necessary parts of a whole, as a composition. By extension, this is a fundamental principle 'that there is no indefinite', and this in turn 'implies the actual infinite'. The existence of the composite means there must be some simpler elements, until we get to the actual infinite [the problem is that the composite looks indefinite, at least until we got to proper chemistry?]. We can argue the point using the notion of causality: what we perceive is an effect, so there must have been a cause, and we must have perceived these however dimly, just as we must have perceived the sound of individual drops of water in a wave. In fact, for Leibniz, the parts are the causes, or rather, 'an argument based on causality and an argument based on parts' must coexist. We know this in principle, but we can also know it in experience and this produces philosophy's 'moment of happiness, [when everything fits] even if it's personally the misfortune of the philosopher'. However, it is also necessary that our experience indicates that we are not always fully organized in our consciousness, or that we can become 'invaded by minute perceptions that do not become... conscious perceptions'. The example is being given a blow on the head, becoming dizzy and disoriented and fainting! Leibniz even thought it might describe the state of death. We can describe this is a state of envelopment, perception without apperception. Leibniz discussed the unconscious, and some of the implications extend even to Freud. However, for Leibniz, the discussion turns on the soul. It has the faculty of apperception, and also one of '"appetition" [the conscious or possibly consciously experienced version of] appetite, desire'. Appetitions correspond to minute perceptions [I can see that the two are at least implicated, they can only develop an appetite for something once you have perceived the objects connected with it]. The work parallels that of an obscure Spanish biologist, Turro, who saw hunger as the global sensation produced by lots of 'minute specific hungers', relating to hunger for proteins, mineral salts or whatever. We can see global hunger as 'integrating' these minute ones [no innocent choice of terms, I am sure]. The way the animals satisfy their hungers is through eating 'minute qualities', grasping not grass but something green, not proteins, but some other object. An internal milieu regulates all these minute perceptions and appetites, in a 'strange communication between consciousness and the unconscious'. In animals, it is instinct that connects appetite to perceptions through a 'psychic investment'. Like us most of the time, animals do not see the mechanism. Leibniz developed his ideas after having read Locke on human understanding, with whom he disagreed. [Apparently he wrote a large book to condemn Locke but did not publish it after hearing Locke had died!] Locke talks about uneasiness as the principle of psychic life, anxiety, [arousal], which constantly 'swarms' through appetite and perception. It might even be God's way of maximizing our perception—or producing continuity again, 'an indefinite progress of consciousness'. Actual unhappiness arises merely from 'unfortunate encounters', which may or may not arise from the best continuity. We can see the links developing between minute perceptions and infinitesimals and differentials. 'Following from this, the Leibnizian unconscious is the set of differentials of consciousness. It's the infinite totality of differentials of consciousness'. Subsequent analyses of the unconscious in philosophy have followed a similar link to infinitesimal analysis, developing a whole 'psycho-mathematical domain'. Both involve symbols. Freud inherited this tradition, but did not develop the idea of unconscious perceptions, except through the notion of unconscious representations, and saw opposition between the conscious and unconscious, not differentials, differences of perception. We can consider Leibniz's approach as a matter of unconsciously detecting minute physical vibrations. The way these are aggregated varies again, because Leibniz has two formulations. The first one is discussed as a relation of parts and wholes, or of composition, where a sense organ totalizes minute perceptions, eyes totalize minute vibrations to compose colours[nice physical vibrations here, of light] . In the second case, Leibniz talks about derivation, not the same as composition, and again we return to infinitesimal calculus and the mathematical notion of the integral, a special kind of totalization, not the same as simple addition. Leibniz talks about augmentation to describe the transition from minute perceptions to something which becomes conscious perception. To proceed further, we have to talk about the relation between the clear and the distinct, and although Leibniz uses the term 'distinct' apparently indistinguishably from terms like notable and remarkable, there is also a technical sense. We can see how this describes the special addition of minute perceptions. Minute perceptions 'form a series of ordinaries, a series called regular', but globalization is different, and not just arithmetical totalization. Instead we are talking about a singularization, something that happens in a particular neighbourhood of a singular or remarkable point, and the result is conscious perception. We have to remember that when we're talking about minute elements, we are talking about differentials, and not concrete elements or specific values, but a relation, as in dy/dx. [Bos elaborates on the difference between integration and addition, and says Leibniz saw the terms as equivalent at first until Bernouilh objected]. We also have to remember that at the singularity, the differential relation changes its sign [always?]. We can make this look like a prelude to Freud if we see the issue as the relation between physical elements and the body indicated by dy and dx. And perception becomes conscious only when this 'corresponds to a singularity, that is, changes its sign'. This in turn depends on the idea of sufficient closeness, of excitation in this case [energetic molecules, so to speak?]. Apparently, Jung displays 'an entire Leibnizian side', via German Romanticism, by introducing an notion of the unconscious as differential, which annoyed Freud and led to the split. So psychic life is also affected by a series of ordinary points reaching the neighbourhood of a singularity, and this is how psychic life itself is composed of the continuous, the extension of points from one singularity to another. This does not just describe 'the universe of the mathematical symbols, but also… the universe of perception, of consciousness, and of the unconscious'. We now have 'the formula for compossibility'. You can trace lines from singularities into the neighbourhood of other singularities, until you get intersecting structures, a continuity. The simplest case is the straight line, but there are other nonstraight lines as well. For example, you can draw two circles that intersect, and argue that 'there is continuity when the values of two ordinary series [along segments of the circles? ]… coincide'. This would be a continuity between two more specific kinds of continuities, just as the square is made up of a continuity of straight lines and vertices. A discontinuity arises if 'the series of ordinaries that derive from singularities diverge'. Thus a whole world is constituted from continuous continuites, 'the composition of the continuous': the best world maximizes continuity. The discontinuity produces the incompossible, arising from divergent series of ordinaries produced by singularities. What makes this difficult to perceive immediately is that 'God is perverse', and disperses these continuities, producing 'leaps, ruptures' in our world, such as the gap between man and animal [apparent only 'to some among us', however]: in fact, God produced all the intermediaries between man and animal, but these are not made visible to us, and might even be 'placed... on other planets of our world'. He did this to encourage us, to help us believe that we could dominate nature, to establish power over nature. And he did at least ensure that we could perceive something of the minute differences, so that we can get some idea of compossibility and incompossibility. This particular world 'mathematically implicates the maximum of continuity' and this is what makes it 'the best of all possible worlds'. A concept is always complex, with 'all sorts of languages that intersect within it': it is 'always necessarily polyvocal'. We can make some progress if we use mathematical apparatus, but philosophical concepts proper are different for Leibniz, and contain 'all sorts of different orders that necessarily symbolize', Including thoughts and experience. Leibniz made a great breakthrough by adding mathematical concepts of the singular to help us see that it was not necessary to oppose it to the universal, but rather to the ordinary or regular. The inspiration might have been mathematical, but a whole philosophical theory emerges: 'don't pay too much attention to the matter of true and false… because what is true and what is false in your thinking always results from something that is much deeper'. It is more important to examine remarkable and ordinary points. If we think only of singular points, there is no extension, and if we use only ordinary points, we get nowhere, and we are not really thinking. [There is no implication for the person, or conventional subject here]—'the more you believe your self to be remarkable (special), the less you think of remarkable points'. When we think of singulars, we necessarily become modest 'because the thinker is the extension onto the series of ordinaries, and thought itself explodes in the element of singularity, and the element of singularity is the concept'. We have to see how Leibniz both creates new principles, and deduces implications from them. We start with the principle of identity which is used to argue that 'Every principle is a reason'it is not just the formal statement that A is A, rather that the thing is what it is, in other words 'identity consists in manifesting the proper identity between the thing and what the thing is'. We might call what the thing is 'the essence of the thing'. So the principle of identity is 'the rule of essences… the rule of the possible'. Another way of putting this is to use medieval terminology and say that the reason is the ratio of essence, ratio essendi [an example of why we need philosophical terminology, and why we must use the terms rigorously, 'exactly the same as scales on the piano'. There is also a hint that we must use these terms for study, and not just as a kind of examination material on philosophy courses. We can give two formulations by Leibniz in each case, a vulgar and a scholarly one. The scholarly formulation of the principle of identity is 'every analytical proposition is true', that is the predicate and subject are identical in analytical propositions. As we saw, the truth of an analytical proposition can be demonstrated 'either by reciprocity or by inclusion', as in the example of the triangle. We can argue that reciprocity involves intuition, while inclusion involves demonstration. The whole exercise is designed to answer the old question 'why is there something rather than nothing?', establishing the reason for being, which depends on the relation (ratio) between the essence and the thing. The principle of sufficient reason, the reason for existing, the ratio existendi. Here the question is 'why this rather than that?'. In vulgar terms everything must have a reason. In scholarly terms we have to leave behind the principle of identity, because that is too formal and abstract, and would permit us to say what a unicorn is even now they do not actually exist. Leibniz argues that every predication, 'the activity of judgment that attributes something to a subject' has a basis in the nature of things. Everything said about a thing is included in the notion of the thing. That includes the essence said about the thing, but also 'the entirety of the affections, of the events that refer or belong to the thing'. We saw above that this means that each individual notion expresses the totality of the world, everything that happens is contained in the individual notion of the thing. We are entering the domain of infinite analysis here, while identities deal with finite analyses. We can think of the notion of the reciprocal, and argue that 'the principle of sufficient reason is the reciprocal of the principle of identity'. However, there is been a significant change in that the principle of sufficient reason now occupies 'the domain of existences'[unlike the reciprocal action we performed with the principle of identity to get tautologies and inclusions]. We have to note that we can only do this if we invoke an analysis extending to infinity, so 'the concept of infinite analysis is an absolutely original notion', and not one that only takes place in the mind of God, but one which we can pin down a bit in the form of a technique of differential analysis and infinitesimal calculus. We also need to remember that Leibniz does not intend here to restore a notion of causality: sufficient reason is more than causality, and we need to 'account for reason in causality itself', and to develop the difference between necessary and sufficient causes: causes are only necessary if they are a part of sufficient reason. Overall, we now have the argument that there is a concept for everything, and this must include relations with other things, including causes and effects. How can we develop this further, again by thinking about reciprocals (not necessarily contradictions or opposites)? In music, the reciprocal might be a musical 'retrograde series'. In philosophy, the reciprocal of 'everything is a concept' is 'for every concept there is one thing alone'. This is an odd reciprocal, more of a necessary implication to make the first statement work. There is no such necessary in finding the reciprocal of the principle of identity: [it is more like a leap into analysis, since there is no necessary reason for all true propositions being analytical]. This, however was a cry from Leibniz [of triumph?] since it leads to infinite analysis, and therefore to the technique and so on. An implication of the notion that for every concept there is only one thing means there can never be two absolutely identical things or that 'every difference is conceptual in the last instance'[that is, related to a concept we have of the thing?] The implications are delirious [no two drops of water can be identical, for example], and contradict classical logic, where the concept is general to encompass a lot of things. We can generalize, but if we analyze deeply enough, we will find that concepts relate to individual things only. This is the 'principle of indiscernibles'. If we take the second formulation, that every difference is conceptual, we only gain knowledge through concepts, the ratio cognoscendi, 'the reason as reason for knowing'. What about other kinds of differences, such as numerical differences? What about differences in space and time that locate particular objects, this chair rather than that one? What about 'distinctions of figure and of movement', or extension and movement—the dimensions that objects occupy, or the speed at which they extend? For Leibniz, these are only matters of appearance expressing conceptual difference—two drops of water 'do not have the same concept'. This is a new way to think about individuation. Leibniz is then faced with the task of showing how bodies take on these particular appearances. One way he does this when discussing Descartes is to suggest that dimensions of mass and velocity are only relative, not enduring principles, that they express something deeper. The same goes for extension, which is not sufficient as a substance in itself: he argues that it is force that manifests itself in figures and extension, force 'is the true concept'. This also connects to the earlier work on trying to develop a mathematics of forces raised to different powers. Specifically, Leibniz is going to argue that force is velocity squared, involving continuous change. Again, he is consistent to the principle of indiscernibles and says 'there are no two similar or identical forces', or that force is [only an abstract] concept. Force is not the same as movement, but 'is the reason for movement'. Mass times velocity squared is a formula for force not movement. Everything will move towards concept of force, including number and the conventional dimensions [expressed in the development of abstract functions for numerical or conventional algebra in the calculus?]. This leads to a fourth principle, this time expressed as a law—the law of continuity. This is more fundamental than a principle. The vulgar formulation says there is no discontinuity in nature. One scholarly alternative says that 'if two causes get as close as one would like, to the point of only differing by difference decreasing to infinity, the effects must differ in like manner'. This is really a way of arguing with Descartes and the view that if two bodies have the same mass and velocity meet, the one with a greater mass or velocity will carry off the other [the argument seems to be instead that differences will decrease to infinity, and there would not be contradictory effects, as Descartes had predicted, either repulsion or continuity of the dominant mass]. But there is another scholarly formulation, that 'in a given case, the concept of the case ends in the opposite case', the 'pure statement of continuity', with examples where concepts of movement end with concepts of rest, given that rest is infinitely small movement [argued above from discussing infinitesimals]. As an alternative, we can say that singularities extend themselves into a series of ordinaries up until the neighbourhood of the next singularity. This is a way of explaining 'the composition of the continuous'. But doesn't this principle contradict the one about discernibles? Not for Leibniz, apparently. The problem is that the principle of indiscernibles refers to determined differences, 'an assignable difference in the concept' itself. The principle of continuity, however refers to progress through vanishing differences, on assignable differences. We need to invoke yet another form of reason, the ratio fiendi, 'the reason for becoming', through continuity. It is necessary again to remember the strange idea that for Leibniz, concepts [meaning notions in this case] are single words expressing the whole world. In normal philosophy, concepts are not a single world but a proposition or a complex, with verbs, implying movement showing the way concept expresses itself. For Leibniz, God has created worlds in which particular individuals do things, but we only express this world in individual notions. The world does not exist in itself, but only in these notions. Yet we can perform an abstraction—the world is going to be a complex curve with singular and ordinary points, with singular as extending into ordinaries and so on. God chooses in order to produce maximum continuity. This is how the world is going to be subjected to the law of continuity, although it is not expressed like that. Each monad can only grasp a small number of singularities, according to its point of view, a small number drawn from the curve of the world produces an individual notion. Different individuals occupy different points of view and therefore encompass some singularities rather than another. [And then, irritatingly, the transcript peters out]. To finish, it is naive to think that philosophers simply hold opposite views or critique each other. We can look at the opposition between Kant and Leibniz. First we have to properly organize the oppositions. Leibniz argues that all propositions are analytical and that this is essential to the progress of knowledge. In the first case, it's not worth arguing about, and philosophy has long preceded by trying to discover what's included in the concept. Kant argues for synthetic propositions, 'in which one of the terms is not contained in the concept of the other', and says that knowledge only exist through the synthetic propositions. For Kant, synthesis means leaving the concept behind in order to pay tribute to it something else, to go beyond the concept How could we decide between the two? It is clear they had both imply certain conceptions of knowledge. For Leibniz, knowledge is based on a particular model of perception or 'passion', something that needs to be apprehended: for Kant, we have to pursue a particular knowledge-act to leave the concept behind. How could we decide between them? It is obviously not a matter of finding facts to support one or the other: philosophical propositions do not depend on the verification of facts. In classic philosophy, there were two questions—quid facti, what was derived from fact and quid juris, what was derived from principle, leading to de jure questions. Leibniz never denies that phenomena are synthetic, that it is possible to encounter qualities of them from experience [the example is this straight line is white] an a posteriori synthesis. But this is based on experience, not knowledge. To know, we must refer propositions to a principle, something that is 'the universal and the necessary' such as that are straight line is the shortest path from one point to another: we know this a priori, we do not need to wait for experience to confirm it [we have defined it as such]. So the issue is whether a priori propositions are analytical or synthetic. Kant says a priori propositions are synthetic, that we leave behind the concept of straight line, to add something to it, a content about it being the shortest path. Leibniz would say that the concept already has this content. For Kant, we have to actually go ahead to draw lines and compare them, in other words to work with a synthesis, which includes extending the notion of straight lines to reach curved lines used in our comparison: when we say the straight line is the shortest path, we are actually comparing straight to curved lines. Obviously, Leibniz is going to disagree, because he has already found, in differential calculus, that the straight line is the limit of curved ones: we have an analytic process, although it tends to infinity. At this stage, it is simply a difference in terminology: what Leibniz calls the difference between finite and infinite analysis, Kant is going to call the difference between analysis and synthesis. It's easy to see why 'good sense' would see philosophical disputes as interminable and irrelevant. However, it is not just a matter of choosing different words, and there are deeper oppositions. In Leibniz's principle of indiscernibles., any difference is ultimately a conceptual one—if two things differ, they cannot have the same concept, and every differences conceptual. This is why we need to analyze concepts, especially to analyze the differences, and this is well developed in the mathematics. Kant, however argues that there are two determinations: one is conceptual, so that the concept represents what the thing is, a lion is an animal that roars, for example. But there are also 'spatio-temporal determinations', which are irreducible to conceptual analysis. Take the example of our two hands. For Leibniz, they differ through the concept. For Kant the issue is whether we are developing an interesting proposition or a platitude. Again, an interest in a proposition cannot be derived from a concept: all the interesting propositions are not found in principle. Spatial determinations cannot be reduced to the concept either—the interesting thing about hands is that they are either right or left, and this is nonconceptual. Dimensions are important in all sorts of interesting ways, because they are now objects to be 'superposed' [one hand placed on top of the other]. The same goes for time which is equally irreducible. For Kant knowing involves synthesizing conceptual and spatio- temporal determinations—he actually called this aesthetic judgement. Here, we have moved beyond just arguing that knowledge involves something more than is contained in a concept—we do this not to affirm another concept, but to leave concepts behind altogether. What has happened here, really, is that Kant has affirmed irreducibility, and he has actually done this by a process of changing 'radically the traditional definition of space and time'. Here again, he departs from Leibniz. Leibniz argued that determinations of space and time are reducible, using different definitions to Kant. The old concept of space saw the matter as one of 'the order of coexistence is or the order of simultaneities', while time 'was defined as the order of successions'. Leibniz wants to push these ideas by asking about possible coexistences and possible successions, and this is going to lead to compossibility. For Kant, there are problems with these traditional definitions, for example because coexistence already implies something about time, but time is not only about succession, but something which refers to the same time. Here, Kant is anticipating a later theory that says simultaneity is a matter of time and not space [I don't know if he means Einstein, or whether this is going to link with his own interest in movement which he identifies with the work of Bergson among others]. Kant is going to go on to say that time actually has three 'modalities'—permanence, succession, and simultaneity of coexistence. Time cannot be defined by privileging succession, nor space through coexistence. This change is significant, because Leibniz's view that you can understand by analyzing concepts depends on the notion of succession, and succession even affects space and time, so 'there is no longer any difference between spatio-temporal differences and conceptual differences'. For Kant, space is a form not a substance, that can be defined by the things that coexist, in exteriority. We can see time as a form of interiority, and this is not just subjective interiority. Again this is to become much more important in later philosophy. Classically, the issue was extension and how it might relate to thought, how bodies might relate to souls. In modern philosophy, it is the relation between thought and time. For Kant, it is a matter of how we relate to an outside. Kant's notion of space is an open one, an aesthetic space because we are no longer confined to logical analysis of the concept, a Romantic space 'because it is the space of overflows', and the space of poetry. The difference between Leibniz and Kant is a difference between the end of the 17th and the start of the 18th century, when an awful lot of other things were changing as well, including the development of Newtonian science, and the French revolution. We can even see that the French revolution finds expression in 'the order of philosophical concepts'. [another missing part of the lecture, because the tape seems to have ended] There is another change that Kant brought about for classical philosophy, 'concerning the concept of the phenomenon'. It used to be the case that phenomenon was simply seen as appearance, sometimes something that was accessible to the senses. It was usually coupled with the notion of essence. As with Plato, this sometimes led to the notion of a duality between appearance in essence, senses and intellect, two worlds, where the world of appearances was a prison, confining our senses and our intellect. Kant uses the word phenomenon differently, to mean 'apparition, that which appears insofar as it appears'. Here, there is an implication that what appears does so in space and time. Apparitions are not related to essences, but to conditions which make them appear, and we have to understand their meaning like this. This is another revolutionary idea, that what appears no longer refers to essences, but to conditions. Concepts don't relate to essences either but to the meaning of the apparition [requiring us to analyze conditions?]. The focus on the meaning of the apparitions produces the new discipline of phenomenology, developed as an autonomous discipline by Hegel. Because there is only a single world, with no other worldly essences, this is also a break between philosophy and theology. Husserl was going to develop a different approach and 'invent a form of logic proper to phenomenology'. Kant was unable to break quite as decisively, and preserved 'the distinction between the phenomenon and the thing in itself'. Leibniz, on the other hand, had developed some of the debates about essence and appearance to develop 'a theory of symbolization', and this was also necessary as a preparation for Kant: 'the phenomenon symbolizes with essence… [it is] no longer… appearance with essence'. There are also new 'disturbances' with subjectivity. Leibniz maintained an alliance with theology, with God having a crucial role in creation. Already there were attempts to bypass the old God of the Word and to begin with infinity, but early attempts to reject creationism were hard to develop. Infinity was one way to extend the possibilities, including the infinitessimal. Descartes uses the notion of subjectivity with his concept of the thinking subject, arguing that a thought must relate to a subject. We can think of the thinking subject as created by God, implying that 'the thinking subject is substance, is a thing… A thinking thing', for Descartes. It would be possible to substitute the thinking subject for God as an infinite thinking subject, but Leibniz and Kant did not do this. For Kant, thinking subjects were not substances, but pure forms, 'form of the apparition of everything that appears'. To say that 'I think' is an empty form 'that conditions every apparition'. This does replace the notion of the divine, however, but this only opens a new problem-- how is the world founded? Leibniz has a particular answer—he 'spoke the discourse of God', founding the existing world [showing us how to understand it?]. This is also the role of classical art, to create 'in the situation of God', 'by organizing milieus'. The romantic artist is not interested in milieu, but territory, leaving territory, heading for 'the bottomless', the ultimate founding. In philosophy, the issue is apparition and the conditions of apparition, once a form of heroic thought. Kant says that the thinking subject is a form that conditions apparition, or the finite ego. And this breakthrough 'depends greatly on the reform' [the Reformation?]. This is a finite foundation itself, not something traceable to an infinite, not a limitation of it, or more of 'an overcoming' of the problem, and the finite is to become infinite, to go beyond itself. We can see the connections with Hegel and even Nietzsche. There is an implication for the problem of identity in Leibniz—now, A is A only if A exists, and 'if there is nothing, A is not A'. Identity becomes hypothetical. Kant wants to go beyond the hypothetical to the thetic—and we only do that by explaining that 'A is A because it is thought', that identity of the thinking subject founds the identity of things, although we have to remember that the thinking subject is the finite ego. What we get is the idea that 'ego equals ego', a synthetic identity, meaning that ego gets its identity by thinking of itself as the condition of everything that appears in space and time. 'Hence the synthetic identity of the finite ego replaces the infinite analytic identity of God'. What would it mean to be Leibnizian today? Kant's new form of thinking established 'a kind of radically new conceptual aggregate', but there are still things in it which are not explained, for example, the 'exact relation… between the condition of the phenomenon itself insofar as it appears' [how do apparitions turn into formed up phenomena?] How does thought condition phenomena? Everything depends on what the form is of thinking. Kant simply has to assert this quality of the thinking subject as a fact of reason, despite his official attempt to make it follow quid juris [all philosophers do this, it seems to me, smuggling in the empirical, usually via some banal assertion]. It follows from some notion that our faculties must be in harmony, especially between passive sensibility and active thought. The idea of God ultimately guarantees this harmony, so God appears after all 'behind our backs'. This is a problem for post-Kantians. Instead, we could show that conditions of apparition are genetic elements in some way. This could proceed through the idea that the finite has some internal mechanism that leads it to try and overcome itself and reach the infinite. Kant did not develop this idea, because he was not particularly interested in the infinite. It is this act of overcoming itself that produces the world of apparitions, as a genetic process not just the conditioning one. In some ways, this involves a return to Leibniz, however: all the elements to explain a genesis are present in Leibniz, including the notion of an unconscious of thought [at the level of perception rather than apperception?]. This unconscious could 'contain the differentials of what appears in thought', and this would be developed by Fichte and then Hegel. Philosophy involves creating concepts, and this is as creative as art: it also occurs 'in correspondence with other modes of creation'. We need concepts as some spiritual accompaniment to a material existence. The old concepts will still prove serviceable as long as we locate them 'within new conceptual coordinates' We use our 'philosophical sensibility' to judge the consistency of concepts. Philosophy has a history which is not separate, and 'nothing, never is anyone overcome'. It is the concepts that we do not create that limit us. Philosophers are no longer seen as heroes—that belonged to the Romantic era. Philosophers no longer attempt to construct or found an entire world. There is a 'kind of continuous flow [with] twists and turns', and we no longer head in that direction. NB the blog also attracted some comments. One person found the whole thing as 'all silly thoughts'. Another commentator tried to analyze the person who had made a comment as intolerant and neurotic.. back to Deleuze page |